Are NBA Policies that Promote Long-Term Competitive Balance Effective? What is the Price?
Abstract
This paper examines competitive balance in the most prominent basketball league in the world: the NBA. Two types of graphs are used. First, long-term competitive balance is studied based on actual positions achieved by the teams on the Regu-lar Season. On the other hand, the competitive balance levels for each season are analyzed using sport betting odds data and through the use of two alternative strategies. In the first approach, density functions for the number of victories for all teams within a season are known, whereas in the second approach, a kernel density function of team winning probability is deter-mined for each season. Thus, a prospective competitive balance analysis is conducted. The study period covers seasons 1993-94 and 2011-12. The results suggest that long-term competitive balance levels are high, as many teams change their classifications. At season level, competitive balance seems to improve along the period studied. However, there are still too many differences between the teams in the same season.
INTRODUCTION
Rottenberg [1], widely considered a seminal work of Sport Economics, examined the domain of Major Baseball League clubs and introduced the “uncertainty of outcome hypothesis”. Later, Neale [2] observed that a world heavyweight-boxing champion (Joe Louis) must challenge the strongest opponent as possible to maximize profits. In this way the paradox Louis-Schemelling was established which arguments that in the professional sport industry, a monopoly is an undesirable market structure, unlike in other markets, in which firms can increase profits when competency is minimized. These studies thus introduced concepts of outcome uncertainty and competitive balance to the Sport Economics field. In another groundbreaking Sports Economics article, Szymanski [3] distinguishes between three types of uncertainty: uncertainty in a game, uncertainty in a season and uncertainty in a competition. Thus, competitive balance is greater if the domain of large clubs is small, if the proximity of teams across seasons is high and if the continuity of team performance is low.
Competitive balance is a key issue of the financial sustainability in sports and it is influenced by the socio-economic contexts of the regions or countries [4, 5]. In general, previous studies have shown that when all other factors remain constant, a competition or league that exhibits a high degree of competitive balance will achieve greater interest from fans [6-8]. In addition, Paul et al. [9] show that more significant differences in team winning records in National Football League games decrease perceived fan satisfaction. In turn, major professional sport league organizations of North America, including the National Hockey League (NHL), National Football League (NFL), Major League Baseball (MLB), and the National Basketball Association (NBA), have implemented a series of regulations that are intended to promote competitive balance [3]. Generally speaking, competitive balance levels are typically higher in these leagues than in other high impact league such as European football leagues [10]. However, variations exist among major North American professional sport leagues, and the NBA is often cited as the less competitive [11-14].
Numerous studies have examined competitive balance levels in sports leagues. In this regard, standard methodologies have employed measures of either dispersion or concentration (e.g., Hirschman-Herfindahl Index, standard deviation of the winning percentage). These measures use final season result based on a retrospective approach. By contrast, measures based on sports betting market data focus on fan expectations for each game and season using a prospective approach [15-18].
The NBA, like other North American sports leagues, employs rules such as draft, free agency or salary cap for to improve competitive balance [19]. However, these rules mainly have long-term effects on competition by altering the distribution of talent and by including new players between seasons. Therefore, in a single season, major differences between teams may be evident, disabling changes in the short term. The aim of this paper is to analyze the extent to which this is true in the NBA. In doing so, both long- and short-term competitive balance is studied in relation to regular seasons of the 1993-1994 season to the 2011-2012 season. The long-term competitive analysis involves an alternation of final team standings. Short-term competitive balance is examined using a prospective approach based on sports betting market data, an emerging trend in the literature.
The remainder of the paper is organized as follows. A theoretical framework on the structure of the NBA and its relation to competitive balance is first presented. This is followed by a brief review of competitive balance measurement methods. Methodologies and measures employed are then explained, and results and a discussion are presented. The paper closes with study conclusions.
National Basketball Association (NBA)
The NBA is the world’s most prominent basketball league, constituting one of the North American Major Leagues together with the MLB, NFL and NHL. Formed in 1946, the league is structured based on a franchise system. It is thus a closed league that differs from European leagues, which largely follow systems of promotion and relegation, and that requires new teams to be approved by the Championship Commission. For this reason, the NBA has included and excluded teams and has changed franchises (teams) between cities throughout its history. In the last season of the present study period, the NBA was composed of 30 teams divided into two conferences (Eastern and Western) that were each divided further into three divisions (Atlantic, Central and Southeast in the Eastern Conference; and Northwest, Pacific and Southwest in the Western Conference). However, at the start of the study period, the league included only 27 teams. Teams play 82 games in a regular season: four games against teams of the same division, three or four games (determined via lottery) against teams of other divisions in the same conference, and two games against teams of the other conference. The eight teams that achieve the most victories in each conference participate in the playoffs and then compete for the championship.
The closed system, which is also employed by the other North American Major Leagues, facilitates the introduction of rules to improve competitive balance under the assumption that ceteris paribus competitive balance increases league attractiveness and thus profits. The NBA has introduced several rules that have been renegotiated over the years by franchises, players and the Commission with the explicit aim to address issues of competitive balance [11]. The most important of these rules are those of drafting, TV revenue sharing, salary capping and luxury taxing.
On the one hand, the draft controls the introduction of new players to the NBA and distributes new players among teams. This system allows the lowest-performing teams of the previous season to select better players. Teams that had played in the playoffs choose the latter, and the rest of the teams enter into a lot to determine the order of picks, in which the worst team has more chances to choose before the other teams. This system’s conduciveness to long-term competitive balance has been demonstrated on several occasions1. For example, the San Antonio Spurs lost 64 games during the 1996/1997 season, affording the team the first position in the next draft. After selecting Tim Duncan, the team reached the playoffs in 1997/1998 and won the championship in 1998/1999. Similarly, the Cleveland Cavaliers, achieving a winning percentage of 0.207 in 2002/2003, acquired LeBron James in the 2003 draft and achieved a winning percentage of 0.427 in the same season. This percentage continued to improve to 0.805, granting the team access to the playoff final in 2008/2009. On the other hand, the NBA distributes TV income equally across all teams. Under the contract signed in 2008, the NBA makes $ 930 million, granting each team $ 31 million.
Finally, the NBA salary cap what the teams can spend to pay their players, which is updated each year. Under luxury tax regulations, the NBA employs another threshold that is slightly higher than the salary cap. If one team exceeds this threshold, it must pay a tax ($ 1 for each $ 1 that exceeds the threshold as of 2005). However, it is not yet clear whether these two regulations significantly affect competitive balance levels in the NBA [20]. Nonetheless, the NBA continues to update these rules to improve competitive balance [11]. These modifications often result in lockouts, which are quite frequent in North American Major Leagues [11]. During negotiations the season lost some games. During the present study period, for instance, teams played only 50 games during the 1998 lockout and 66 games during the 2011 lockout.
Competitive Balance Measurement
Competitive balance has been measured in numerous ways in the scientific literature. Such measures include the standard deviation of the winning percentage adjusted to the standard deviation of perfect competitiveness [3, 10, 21, 22], the Herfindahl-Hirschman Index [23], the same index adjusted for perfect competitiveness regarding to the number of teams [24-27], the Gini-coefficient [28] and the winning concentration ratio [29]. All of these methods use scores obtained at the end of a season as a data source (i.e., retrospective data). Other methods utilize prospective data obtained from the sports betting market. These measures are based on expectations and perceptions of what could happen during each game or season. The first studies that employed sports betting data examined competitiveness levels in the English Premier League matches [30, 31]. Following these studies, it is possible to find studies that employed sports betting data to examine game result uncertainty and its relation to attendance [32-34]. Recent studies have subsequently applied this kind of data at game level, using measures such as Theil Index [7]. This index is useful for testing the outcome uncertainty of a single match, and it can be used to evaluate their influence on attendance [35, 36]. However, to test the competitive balance at season level with sport betting odds data, it is necessary other kind of measures. In this way, Paul et al. [15] presented the first research that use sports betting market data to examine league competitive balance, plotted the average of favorite odds over several seasons to determine perceived competitive balance levels in Major League Baseball. Bowman et al. [16, 17] also used sports betting market data to evaluate NFL, NBA and MLB competitive balance levels and their evolution through several measures. Finally, del Corral [18] plotted the distribution of the expected number of points from betting odds to examine competitive balance in major European soccer leagues.
This approach assumes that betting odds serve as unbiased estimates of result probabilities. While some papers have identified biases in betting odds [37, 38], this does not preclude their ability to calculate accurate probabilities because while there is no consensus in the literature on whether betting odds are efficient, Forrest and Simmons [39] and Sauer [40] state that at least weak efficiency appears to characterize this market. Hence, Buraimo et al. [41] recommend the use of sports betting odds to study uncertainty outcomes over other measures. On the other hand, Bowman et al. [17] explain that point spreads are the most unbiased predictors of individual game outcomes and that betting market inefficiencies have been eliminated overtime as they were identified by the bettors. Therefore, Bowman et al. [17] defend the utility of point spreads for examining the competitive balance of an entire league season.
However, Kringstad and Gerrard [42] argue that the complexity of the leagues’ structures in team sports due to their multiple prizes requires alternative competitive balance measures to conceptualize this problem. In this way. The competitive balance measured by an individual indicator shows only a punctual information. Nevertheless, there are other ways to work with betting odds data [18], favoring a more visual interpretation in which more information can be drawn with a single analysis. These approaches could help the practitioners to analyze the competitive balance of each season and the reasons that are behind. In addition, the description and use of new methods for measuring competitive balance are important study areas for improving the research agenda.
While the above listed approaches are used to study an individual game or season, competitive balance can be evaluated over a long-term period as well. Long-term measures of competitive balance are less frequently applied and are less varied. The most commonly used method involves measuring the number of teams that won the championship in a determined period [10, 11]. It can also be found studies that use time series and structural breaks tests to analyze the changes in the competitive balance in different sport leagues [4, 19, 43-46]. However, methods involving the HHI, standard deviation of win percentages [10, 11, 26] and variation and evolution of positions for all teams in a regular season for a determined period can be employed as well.
NBA Competitive Balance
The competitive balance of NBA has been studied in different range of dates and using different kind of methodologies. Some papers are focused on match day level, with the aim to analyze the effect of competitive (im) balance on attendance [47, 48]. On the other hand, some articles that analyze NBA competitive balance at season level and in long-term argue that NBA is probably the North American Major Sport League with less competitive balance [11-14]. Berri et al. [49] explain that one of the major problems in the talent distribution in NBA is that the morphological characteristics of the elite players are very rare. There are short supply of tall people in the population. For these reason, some teams always have more talent, and the owners can do nothing to solve this constraint. Additionally, basketball has a game system that fortifies this problem. The most players in NBA are not stars, and most of wins are produced by a minority of NBA players, 20% of the players produced 70% of the wins [50]. This fact is an important feature, because only one player could make more differences than in other sports.
Moreover, there are some studies that demonstrate that factors such us salary caps or luxury taxes do not have impact in competitive balance of NBA [19, 20, 27]. These findings could be related with other studies that find that the European Basketball Leagues, which have much less strict rules, like ACB in Spain, have a competitive balance at season level nearest to NBA [51, 52]. However, in general terms, the competitive balance of NBA can still be classified as high [52]. Recent studies suggest that NBA improved their competitive balance in the past 20 years [17]. For these reasons, it is important to add new research that show more information about the properties of NBA competitive balance both short and long terms.
MATERIALS AND METHODS
To determine competitive balance levels in the NBA, we examine seasonal and long-term competitive balance trends. In both cases, competitive balance was evaluated from 1993/1994 to 2011/2012 (i.e., 19 seasons). The competitive balance season by season was measured using a prospective approach and sports betting odds, based on a visual interpretation. More specifically, point spreads of NBA games were used. In spread betting, the bookmaker ascribes an advantage to the underdog (handicap) and a disadvantage to the favorite (supremacy), resulting in an implied probability of 50% for both sides of the wager. As only two possible outcomes are possible in the NBA (home and away victory), game betting odds of 1.90 are applied to both teams to ensure an over round of bookmakers. For example, Oklahoma City Thunder’s supremacy over the Sacramento Kings after the last game of the 2011-2012 regular season held in Oklahoma was valued at 10. This implies that for this game, Oklahoma City Thunder was the clear favorite.
The database comes from the webpage www.covers.com and it was facilitated as a datasheet by a professional bookie, Leigh Herdman. It includes game results, dates, local teams, away teams and supremacy data from approximately 25,000 observations. The data that this webpage provide are the closing consensus line obtained from the most common line offered across a selection of bookmakers2. With point spread data, embedded winning probabilities cannot be obtained directly as using money lines3 but they can be estimated by using probit models. Particularly, one probit model was estimated for each season in which the dependent variable valued at 1 if the local team wins and with supremacy serving as the independent variable.
Probit model results are shown in (Table 1). As predicted, supremacy achieves positive and significant coefficient, implying that supremacy increases home victory probability. Once these probits are estimated, models can predict the probability of a home team win. Fig. (1) shows the relation between supremacy and the predicted probability of a home team win.
Using home and away victory probabilities for all games, two prospective measures of competitive balance were employed. The method developed in del Corral [18], which focused on European soccer, was applied first. Del Corral [18] calculated the probability of three possible soccer match outcomes (i.e., home victory, tie, away victory) through money lines, with the objective to evaluate their competitive balance with a prospective approach. In a soccer game, the winner obtains three points and the loser wins no points, and if a game finishes in tie, both teams obtain one point. Assuming that match results are independent of one another so that the joint probability of two events is equal to the product of the two probabilities, the probability of each team obtaining a certain number of points in the final standings was calculated. Hence, it was in turn possible to formulate a single chart with all team score probabilities, thus revealing the competitive balance level of each season. Higher concentrations of lines in the chart correlate with higher levels of competitive balance in a season. Using this method, a chart listing probabilities of achieving different numbers of victories for all teams at the end of a regular season was created to determine competitive balance levels in the NBA from 1993/1994 to 2011/2012. Secondly, a kernel chart with probabilities of victory averages for each season was also created. With this chart, it can be compared results of the previous measure with the distribution of average team victory probability. This approach overcomes shortcomings of the density function approach in that closeness between teams is not affected by the number of matches played. These figures present a straightforward result: higher kernel dispersion correlates with lower competitive balance. It is important to note that, to our knowledge, this approach has never been employed in the literature.
Probit estimates of home victory 1993-2012.
| Season | 93-94 | 94-95 | 95-96 | 96-97 | 97-98 | 98-99 | 99-00 | 00-01 | 01-02 | 02-03 |
|---|---|---|---|---|---|---|---|---|---|---|
| Constant | -0.08 | -0.07 | -0.04 | -0.13 | -0.04 | 0.05 | -0.03 | -0.08 | -0.05 | 0.03 |
| Supremacy | 0.10 | 0.09 | 0.10 | 0.11 | 0.10 | 0.09 | 0.10 | 0.10 | 0.09 | 0.09 |
| Pseudo R2 | 0.17 | 0.13 | 0.16 | 0.21 | 0.19 | 0.12 | 0.14 | 0.13 | 0.10 | 0.11 |
| Number of observations | 1,184 | 1,180 | 1,257 | 1,261 | 1,260 | 791 | 1,264 | 1,260 | 1,260 | 1,277 |
| Season | 03-04 | 04-05 | 05-06 | 06-07 | 07-08 | 08-09 | 09-10 | 10-11 | 11-12 | |
| Constant | 0.00 | -0.06 | -0.03 | -0.06 | 0.00 | -0.06 | -0.06 | 0.09 | -0.06 | |
| Supremacy | 0.09 | 0.10 | 0.10 | 0.09 | 0.10 | 0.11 | 0.10 | 0.08 | 0.10 | |
| Pseudo R2 | 0.10 | 0.14 | 0.11 | 0.09 | 0.16 | 0.16 | 0.14 | 0.11 | 0.13 | |
| Number of observations | 1,271 | 1,314 | 1,319 | 1,331 | 1,316 | 1,315 | 1,312 | 1,311 | 1,074 |
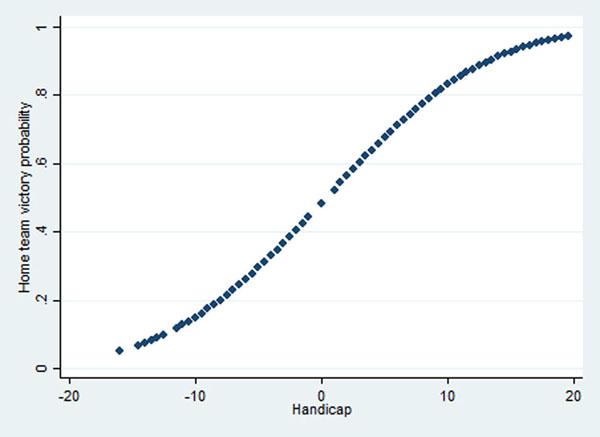
Relation between supremacy and the probability of a home team win for the 1995-1996 season.
However, strong seasonal competitive balance can occur in the presence of poor long-term competitive balance. Alternatively, poor seasonal competitive can occur in the present of strong long-term competitive balance if positions achieved by teams vary considerably across seasons. In illustrating long-term competitive balance in the NBA, final rankings for each team in a regular season were plotted along a temporal line based on a moving average for three seasons.
Finally, we have also calculated additional measures to complement the previous ones, with the aim of improving the consistency of the interpretations. On the one hand, the Herfindahl-Hirschman Index (HHI) and the standard deviation of winning percentage were implemented [5], but using the expected number of victories [12]. On the other hand, we calculated the average position change with respect to the next season in the NBA and BBVA League. In addition, we also included the average position change for the top 4 with respect to 3 seasons apart.
RESULTS AND DISCUSSION
The results on long-term competitive balance are shown in Fig. (2), wherein charts show the evolution of final standings for the teams in a regular season based on three-year moving averages. More pronounced fluctuations in team rankings throughout a season are associated with better long-term competitive balance.
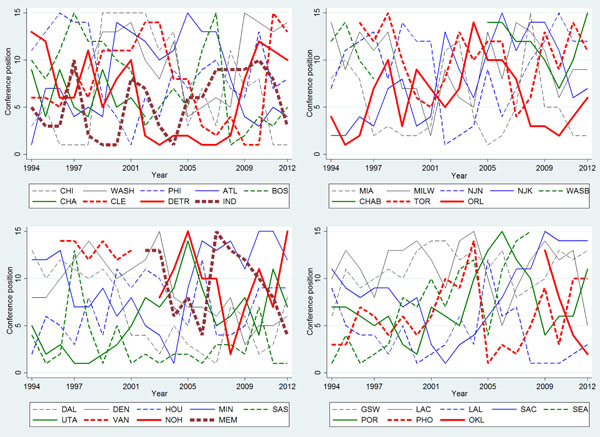
Long-term competitive balance graphs.
Note: CHI- Chicago Bulls, WASH- Washington Wizzards, PHI-Philadelphia 76ers, ATL- Atlanta Hawks, BOS- Boston Celtics, CHA- Charlotte Hornets, CLE- Cleveland Cavaliers, DETR- Detroit Pistons, IND- Indiana Pacers, MIA- Miami Heat, MILW- Milwaukee Bucks, NJN- New Jersey Nets, NJK- New York Kincks, CHAB- Charlotte Bobcats, TOR- Toronto Raptors, ORL- Orlando Magic, DAL- Dallas Mavericks, DEN- Denver Nuggets, HOU-Houston Rockets, MIN- Minnesota Timberwolves, SAS- San Antonio Spurs, UTA- Utah Jazz, VAN- Vancouover Grizzlies, NOH- New Orleans Hornets, MEM- Memphis Grizzlies, GSW- Golden State Warriors, LAC- Los Ángeles Clippers, LAL- Los Ángeles Lakers, SAC- Sacramento Kings, SEA- Seattle Supersonics, POR- Portland Trail Blazers, PHO- Phoenix Suns, OKL- Oklahoma City Thunder.
The charts show lines that are mixed together with very random evolutions. This difficulty in clearly identifying the lines is a result itself. In this way, it is evident that, in both conferences, teams fluctuate in rank frequently. For instance, all teams occupied the non-playoff and playoff zones (eighth place). There are clearly example cases for the study period. Boston Celtics finished the regular season as the worst team of its conference in 2006/2007 season. The next season finished as the team with more victories in the conference and won the championship. On the other hand, Chicago Bulls finished on the first position in its conference and won the championship three consecutive seasons (1995/1996 season to 1997/1998 season). However, the next four season finished the last one in its conference. In 2004/2005 season, the team returned to qualify for playoffs. Moreover, no team has always finished in one of the top five positions in a respective conference. This is not the case for Spanish football and basketball leagues, as Real Madrid and FC Barcelona have occupied in the highest rankings. Long-term competitive balance is thus quite high, as teams are likely to fluctuate in rank. Rather, there are no good or bad teams, but teams that exhibit good or bad performance. Hence, some policies implemented in the NBA have been effective in terms of maintaining long-term competitive balance.
Table 2 allows us to confirm this assumption. We can see that the average position change varies similarly in NBA Conference and in BBVA League (we must take into account that BBVA conference has 20 possible positions and NBA Conferences only has 15). However, if we check the average position change 3 seasons apart of the top 4, NBA varies more than BBVA League.
Average position change in NBA and BBVA League.
| Season | NBA | NBA top4 (3 Seasons apart) | NBA Conference | BBVA | BBVA top4 (3 Seasons apart) |
|---|---|---|---|---|---|
| 1993-1994 | 5.04 | 3.00 | 2.44 | 2.47 | 4.50 |
| 1994-1995 | 4.26 | 5.75 | 2.26 | 5.21 | 4.50 |
| 1995-1996 | 4.90 | 12.00 | 2.55 | 4.26 | 4.75 |
| 1996-1997 | 5.45 | 12.50 | 2.55 | 3.82 | 5.50 |
| 1997-1998 | 6.83 | 11.50 | 3.38 | 3.59 | 6.00 |
| 1998-1999 | 4.90 | 7.00 | 2.55 | 4.19 | 4.75 |
| 1999-2000 | 4.14 | 5.50 | 2.21 | 3.88 | 2.67 |
| 2000-2001 | 6.32 | 6.25 | 3.14 | 3.53 | 3.50 |
| 2001-2002 | 4.21 | 6.50 | 2.14 | 4.00 | 4.25 |
| 2002-2003 | 5.59 | 7.50 | 2.90 | 4.00 | 7.00 |
| 2003-2004 | 8.34 | 12.50 | 4.34 | 3.71 | 4.00 |
| 2004-2005 | 5.62 | 10.00 | 3.07 | 4.00 | 3.25 |
| 2005-2006 | 5.80 | 8.50 | 3.07 | 3.53 | 3.25 |
| 2006-2007 | 5.76 | 8.00 | 2.97 | 4.18 | 0.50 |
| 2007-2008 | 5.66 | 7.50 | 3.14 | 2.65 | 1.75 |
| 2008-2009 | 4.87 | 11.25 | 3.00 | 3.29 | 2.25 |
| 2009-2010 | 6.07 | 9.00 | 3.13 | 4.18 | 0.75 |
| 2010-2011 | 4.47 | 3.25 | 2.50 | 4.59 | 4.00 |
| Average | 5.46 | 8.19 | 2.85 | 3.84 | 3.73 |
The theory of competitive balance determines that talent (players) must be shared among different teams. This principle is more difficult to follow in basketball, as only ten players (5 vs. 5) play at a given time, and the addition of one outstanding player can significantly change the sport productivity of a team [50]. However, it has been shown that long-term competitive balance appears quite high, as regulations maintain the distribution of talent as much as possible, facilitating the addition of prominent players to the lowest performing teams. However, it is also interesting to determine whether these policies are also effective in the short term. This would imply that teams exhibit similar strengths in a given season, which may be more important to fans.
In order to analyze the short-term competitive balance levels, the following graph presents competitive balance results generated through density functions obtained from point spread data converted to probabilities Fig. (3). In turn, seasonal competitive balance levels can be interpreted. High dispersion among the curves denotes low competitive balance. This would mean a league with predefined positions where the surprise is very difficult to occur in the final standing of the Regular Season. In cases of high competitive balance, teams differ only marginally, rendering it difficult predict final competition classifications for a regular season. Moreover, as a team’s likelihood of reaching first place is not reflective of the full spectrum of team goals, probabilities of reaching the playoffs must also be examined [42]. For this reason, although this method is not interpreted directly quantitatively, as happens with other methods, it allows not only to extract more information but also to explain more in depth the characteristics that differentiated each season. The charts provide another point of view throughout a visual interpretation that could improve and complement the traditional methods in future researches. In addition, these methods could provide more information to practitioners and managers. They are interested, not only in a punctual competitive balance data, but also in information about the dispute of playoffs, identification of clearly favorites and underdog teams, or teams that have been underestimated or overestimate. But, still, several measures of competitive balance can be calculated the expected number of victories instead the actual number of victories [16, 17]. Bowman et al. [17] argue that the expected wins not only have the advantage of capturing fan perception but are the best measure of the real underlying quality differences between teams without the noise of how the season is actually unfolding.
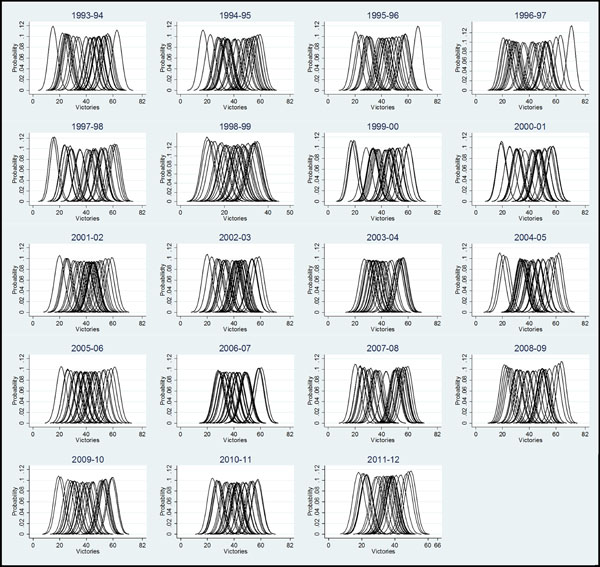
Short-term competitive balance graphs: Number of victory densities.
The following charts allow one to examine competitive balance attending to these properties.
It is evident that the league is characterized by several seasons of low competitive balance. For instance, for the 1993/1994 season, one team is set apart in both sections of the chart. The 1994/1995 season reveals two distanced teams as well, but only along the left hand section of the chart. In addition to this, in both seasons there was a high dispersion of the functions, with a lot of teams being given no opportunity to rank in the first positions. This result is consistent for the entire study period, which represents a problem in the outcome of the application of rules such as salary caps, which would have a positive effect in the competitive balance at season level. In this way, previous studies have not provided evidence of the influence of salary caps on NBA competitive balance [20, 27].
Similar trends are observable for other major leagues that do not employ regulations as stringent as those of the North American Major Leagues, such as European soccer leagues. As with NBA teams, some teams cannot reach the highest positions and other teams differ considerably in rank from the majority in the BBVA League (Spain), Premier League (England) and Bundesliga (Germany), as demonstrated by del Corral [18], who used a similar methodology as that employed in this study based on betting odds.
Coming back to the season by season analysis results show a favorite team for the 1995/1996 and 1996/1997 seasons, with considerable difference in probabilities of achieving first place. The 1998/1999 season coincides with the first lockout period. This season exhibits good competitive balance in relation to other seasons. However, we cannot make objective comparisons between this season and the other seasons, as other factors must be considered and teams played 16 fewer games [11].
The 1999/2000 to 2002/2003 season period exhibits slightly better competitive balance than the earliest seasons analyzed. Fort and Lee [19] determined that in relation to other periods of North American professional sport league labor dispute, competitive balance increased following the 1998 NBA lockout. However, our results suggest that several teams were afforded no apparent opportunity to enter playoff positions, reflecting poor competitive balance. Nonetheless, the 2003/2004 season exhibits the highest degree of competitive balance for the analyzed period.
A decline in competitive balance has occurred since the 2004/2005 season respect with the previous one. Density functions show more distanced teams along both sides of the chart, revealing the presence of favorite and underdog teams. This season corresponds with one of the most important changes realized in the NBA competition system, which may have contributed to the dispersion of the teams in the next seasons. The NBA divided each conference for two divisions into three divisions, and teams of the same division began to play four times in each division. Therefore, divisions with strong teams can have a negative effect on competitive balance via the introduction of new teams, as in the case of the introduction of the Charlotte Hornets. Hence, changing the structure, and the incorporation of new teams, alters patterns of competitive balance. Fort and Lee [19], who also studied the breakpoints in the competitive balance of North American Sport Leagues, confirmed greater correspondence due to expansions and team relocations than with the rule changes.
However, the end of the period shows grater competitive balance than in the start. Bowman et al. [17], who analyze competitive balance of NBA with six measured developed from betting odds, show an improvement in the same period. This comparison indicates that the results obtained by density functions allow to extract similar interpretations than the obtained ones with other indicators. However, they also allow to extract other kind of information at the same time. In addition, Table 3 contains the results of the HHI and standard deviation of winning percentage, and the same conclusion can be recovered. The competitive balance is better at the end of the analyzed period. Nonetheless, big differences between teams can be still distinguished.
Competitive balance measures using expected victories.
| Season | HHI | SD |
|---|---|---|
| 1993-1994 | 0.040 | 12.8 |
| 1994-1995 | 0.040 | 11.4 |
| 1995-1996 | 0.037 | 12.3 |
| 1996-1997 | 0.038 | 14.1 |
| 1997-1998 | 0.038 | 13.5 |
| 1998-1999 | 0.037 | 6.6 |
| 1999-2000 | 0.037 | 11.4 |
| 2000-2001 | 0.037 | 11.2 |
| 2001-2002 | 0.036 | 9.7 |
| 2002-2003 | 0.036 | 10.0 |
| 2003-2004 | 0.036 | 8.8 |
| 2004-2005 | 0.036 | 10.9 |
| 2005-2006 | 0.035 | 9.7 |
| 2006-2007 | 0.035 | 9.1 |
| 2007-2008 | 0.036 | 12.0 |
| 2008-2009 | 0.036 | 12.2 |
| 2009-2010 | 0.036 | 11.6 |
| 2010-2011 | 0.035 | 9.7 |
| 2011-2012 | 0.036 | 8.9 |
In further illustrating short-term competitive balance analysis results, Fig. (4) presents kernel densities of average victory probabilities for all teams and for each season. The results reinforce previous findings. The 2003/2004 season shows the highest degree of short-term competitive balance, with a kernel function mode close to 0.5 and with limited dispersion. On the other hand, the 1996/1997, 2007/2008 and 2008/2009 seasons exhibit the lowest levels of competitive balance.
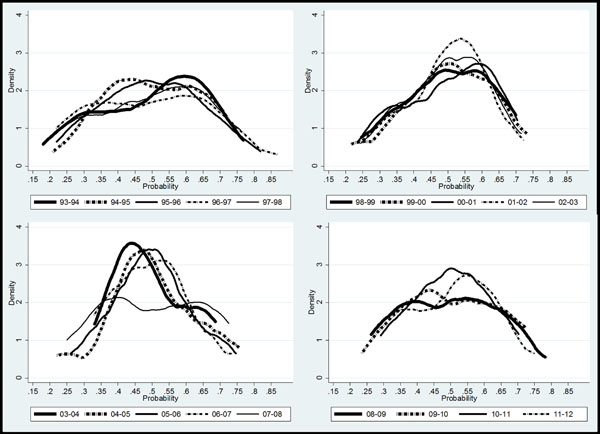
Short-term competitive balance graphs: Winning probability kernels.
CONCLUSION
This paper has studied long- and short-term competitive balance in the NBA. Graphs produced on long-term competitive balance showed a high level of competitive balance in the Regular Season. This result is reinforced by the fact that 17 different teams have reached the NBA finals over the 19 seasons analyzed. It can thus be concluded that long-term competitive balance in the NBA is high and that policies designed to achieve this objective have been effective. However, the results reveal poor competitive balance in the short-term (i.e., season to season). That is, NBA fans are afforded long-term competitive balance at the expense of short-term competitive balance. This raises questions regarding whether NBA fans prefer long- or short-term competitive balance. This research question merits further exploration, because if fans value short-term competitive balance, the NBA Commissioner must adapt NBA policies in order to get not only long term competitive balance but also short term competitive balance.
From a methodological point of view, this paper presents a promising approach to competitive balance measurement that utilizes betting odds data. We are confident that future studies will be quick to adopt this novel approach.
1 Long-term competitive balance refers to an assumption that teams are likely to change their positioning in a league to prevent the league from being dominated by a few teams.
2 It is important to note that some recent studies that analyze NBA competitive balance, use data from this source [17, 47, 48].
3 In [16] is explained a method to convert money which lies in embed-ded probabilities.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This paper is a revised version of the undergraduate thesis of Fernando Herencia-Quintanar. The authors would like to express their gratitude to Verónica Baos León for her language revision. The authors also acknowledge the Consejería de Educación, Cultura y Deportes de la Junta de Comunidades de Castilla-La Mancha and Fondo Europeo de Desarrollo Regional (Project PPII-2014-004-A) for the financial support of the article.


