Methodological Differences in the Interpretation of Fatigue Data from Repeated Maximal Effort Knee Extensions

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Methodological Differences in the Interpretation of Fatigue Data from Repeated Maximal Effort Knee Extensions

Anthony B. Ciccone Jake A. Deckert Trent J. Herda Philip M. Gallagher Joseph P. Weir, * Open Modal
Authors Info & Affiliations
The Open Sports Sciences Journal • 28 Apr 2017 • RESEARCH ARTICLE • DOI: 10.2174/1875399X01710010037

Abstract

Background:

Isokinetic fatigue protocols are commonly used in both research as well as in kinesiology education. However, fatigue quantification methods vary between studies.

Objective:

Therefore, the purpose of this study was to determine how fatigue quantification methods affect data interpretation and which methods may be most appropriate.

Method:

In this study, we quantified fatigue from a repeated maximal effort isokinetic knee extension test using different methods, as seen in published research. Nine healthy males and nine healthy females performed 50 concentric knee extensions at 180°•s-1. For each repetition, torque was quantified as either peak torque (PT), torque at the mid-point of the range of motion, and torque integrated over the full, middle 30° range of motion, and isokinetic range of motion. Fatigue Index was quantified using either the first and last three or five repetitions or the peak and last three or five repetitions. Torque slopes were quantified using all repetitions or repetitions that occurred at and beyond the repetition at which the greatest torque value occurred.

Results:

There was a significant inverse relationship between angle at PT and repetition number. Measures of fatigue were overestimated when torque integral over the isokinetic range of motion was utilized. When the first three or first five repetitions were utilized for Fatigue Index calculations, fatigue was underestimated.

Conclusion:

Results suggest that torque integral over the full range of motion is likely the best representation of strength or work. Also, researchers should omit the first few repetitions from their quantification of Fatigue Index or torque slope.

Keywords: Thorstensson, Biodex, Dynamometer, Torque, Force, Isokinetic.

INTRODUCTION

Isokinetic fatigue protocols are commonly used in both research [1-11] as well as in kinesiology education [12]. A classic study by Thorstensson and Karlsson [7] examined if the development of fatigue is related to the muscle fiber type composition. The fatiguing task included torque measurements over 50 and 100 repeated maximal effort isokinetic knee extensions performed at 180°•s-1. Fatigue was quantified by calculating the percent decline in torque between the average of the first three repetitions and repetitions 48-50, and this calculation was referred to as the Fatigue Index. This Fatigue Index was found to be related to muscle fiber composition of the vastus lateralis. Researchers have since utilized similar repeated maximal effort isokinetic tests to examine the relationship between torque measures and other measurements such as electromyographic and mechanomyographic signals [2, 3]. Furthermore, practitioners can make use of repeated effort isokinetic tests to investigate fatigue-induced injury risk in athletes [13] and to compare individual players’ performance to that of established normative data from elite athletes [14].

The “constant velocity” feature of isokinetic knee extensions allows researchers to use velocity as a valid independent variable. However, isokinetic dynamometer repetitions do not occur at the target velocity at the beginning and ending of every repetition [15, 16]; the isokinetic portion of each repetition is known as the load range. Furthermore, the appropriate measurement of biometrics such as electromyographic and mechanomyographic signals requires the use of range of motion (ROM) windows. Thus, it may be problematic to relate an instantaneous value such as peak torque (PT) to another measurement that was taken over a window of time. However, measuring torque variables over each repetition’s full range of motion (ROM) will contain information from non-target velocities [15, 16]. Some researchers have made an effort to ensure that they only measure isokinetic data by analyzing data that lies within the load range. This is usually achieved by limiting the data window to a segment that is well within the load range, often spanning approximately 30 degrees around the mid-ROM position [1-4, 11, 17]. In at least one study, the load range of each repetition was identified and torque during that window was used to quantify fatigue during a fatiguing isokinetic protocol [5]. However, many researchers collect data from the full ROM of each repetition or do not report their measurement window [6, 18, 19].

Furthermore, once a torque variable is calculated, fatigue quantification methods may differ. For example, some studies use the averages of the first and last three to five repetitions [7, 11, 20, 21] to calculate Fatigue Index whereas, others have used averages of the highest repetitions and last repetitions to calculate Fatigue Index [3, 8], and others have used a completely different metric, torque or work slope [9, 22-25], which has also not been quantified in a consistent manner. The lack of consistency between-study measurement windows and analysis methods may lead to differing interpretations of the same data. Importantly, torque variables collected from different measurement windows may also have closer relationships with other variables of interest. Therefore, the purpose of this study is to investigate the effect of measurement window on torque and fatigue-related variables.

MATERIAL AND METHOD

Subjects

Nine healthy males and nine healthy females (age=21.1±1.4 y; height=173.8±12.4 cm; mass=72.1±14.7 kg) participated in the study. Exclusion criteria included current or past neuromuscular or musculoskeletal injuries as well as any metal implants above the neck, besides common orthotic braces, and being non-recreationally trained (defined as exercising less than twice per week or exercising more than four times per week). Each subject signed an informed consent document before completing a health history questionnaire. The study was reviewed and approved by The University of Kansas Human Subjects Committee.

Experimental Design

Subjects visited the lab on two occasions, one familiarization visit and one experimental trial. Subjects refrained from strenuous exercise in the 24 hours prior to each experimental visit. During the familiarization visit, subjects were exposed to the relatively uncommon task of isokinetic knee extensions. This visit decreased the likelihood of the learning effect occurring during experimental trials. During experimental trials, subjects performed 50 maximal effort knee extensions at 180°•s-1. External torque and dynamometer position were collected for the duration of each experimental trial. Using custom-written LabVIEW (National Instruments Corporation, Austin, TX) programs, external torque data from each repetition were analyzed using five different parameters, as described below in the Signal Processing section.

Isokinetic Protocol

Subjects were seated and secured into a Biodex System 3 Pro Isokinetic Dynamometer (Biodex Medical Systems Inc, Shirley, NY) with their right knee joint in-line with the dynamometer arm axis-of-rotation, the bottom of the dynamometer arm pad approximately two inches above the foot, and a hip angle of 100°. Dynamometer ROM bottom stop was set at an arm angle of 90° (perpendicular to the floor) and the top stop was set at full knee extension (knee angle reference = 180°). The dynamometer was operated in isokinetic mode at a velocity of 180°•s-1. For each repetition, subjects performed voluntary knee extensor contractions from the bottom stop to the top stop, and then they relaxed as their leg fell from full extension back to the bottom stop. Subjects warmed up by completing five submaximal repetitions at the testing velocity. After resting for at least 30 seconds, subjects began performing maximal effort knee extensions. To increase the likelihood of measuring true maximal effort knee extensions, strong verbal encouragement was provided during all maximal effort knee extensions.

Signal Processing

Using a custom-written LabVIEW program, torque, position, and velocity data were simultaneously sampled at a rate of 10k Hz. Using a 4th order zero lag Butterworth digital filter, torque data were low pass filtered at 6 Hz. Velocity data were low pass filtered at 15 Hz. Position data were low pass filtered at 100 Hz. Using the peaks and troughs of the position signal, each repetition was segmented into concentric and passive lowering phases. PT was measured as the highest filtered torque value from each concentric phase, and position at peak torque was also measured. Torque data were captured by: 1) including data between the trough and peak of the position signal (F = full range of motion), 2) excluding torque data that occurred at a velocity less than 179.25°•s-1 of each concentric phase (L = load range), and 3) by excluding torque that occurred outside of the position data spanning from 120°-150° of each concentric phase (M = middle range of motion). Torque was also measured at the concentric-phase dynamometer arm angle of 45° from the horizontal plane (T135), by calculating the torque integral or the area under the torque curve over F (TIF), M (TIM), and L (TIL) ROMs. All torque data were normalized to a percent of the peak value achieved in each test.

Fatigability Analysis

Fatigue responses were quantified using two general methods: 1) calculation of the Fatigue Index, and 2) calculation of torque slopes using subject specific regression analyses.

Fatigue Index

Decrements in torque variables across repetitions were calculated by analyzing changes in TIF, TIM, and TIL windows, PT and T135. Fatigue Index was calculated using the following general formula: [(initial torque-final torque)/initial torque]*100. To calculate the initial torque and final torque values to be used in the Fatigue Index formula, several approaches from the literature were examined. For the initial torque, the average of either the first three repetitions, average of the first five repetitions, the highest three-repetition average, or the highest five-repetition average values were used. The average of either the last three or last five repetitions was used for final torque. Eight different combinations of initial torque and final torque were calculated by using the average of the torque values from the first three and last three repetitions (F3), the first five and last five repetitions (F5), the highest three repetitions and last three repetitions (P3), the highest five-repetitions to the last five (P5). Each of the four Fatigue Indexes was calculated using the five different torque variables (PT, T135, TIF, TIM, and TIL). In addition, it is common for isokinetic fatigue protocols to analyze either 30 or 50 repetitions, so we have incorporated analyses of repetition ranges of both 1-30 and 1-50 repetitions.

Torque Slopes

For the torque slope calculations, on a subject-specific basis, the torque variables were regressed against repetition number, which yielded subject-specific slopes and Pearson r values for each regression. All five torque variables were regressed against repetition number using repetition ranges of 30 or 50. Because the first repetition typically exhibits a lower torque value than the second repetition (10), the initial repetition used in the regressions was either the first repetition or the repetition with the highest PT (FPT).

Statistical Analyses

For each trial, isokinetic load range and angle at PT were separately regressed on repetition number to yield subject-specific slopes, the means of which were compared to zero using independent t tests and associated 95% confidence intervals. Because Pearson r values cannot be directly analyzed using ANOVA, individual r scores were converted into Z-scores before any statistical analyses were performed on r data [26]. Each Fatigue Index was analyzed using a 4 (calculation method: F3, F5, P3, and P5) x 2 (repetition range: 1-30 and 1-50) x 5 (torque variable: TIF, PT, T135, TIM, and TIL) repeated measures ANOVA. Slope and Pearson r (Z-score) scores of torque variables across repetitions were analyzed using a 2 (initial repetition position: highest PT and first repetition) x 2 (repetition range) x 5 (torque variable) repeated measures ANOVA. The Huynh-Feldt correction was used to compensate for violations of sphericity. Partial eta squared was used to quantify the effect sizes. Following significant interaction effects, tests of simple effects were employed and 95% confidence intervals were used to examine pairwise comparisons where appropriate [27]. Alpha values were set at 0.05. SPSS Version 22 was used for all ANOVA and follow-up calculations. All data are presented as means and SD, unless otherwise noted.

RESULTS

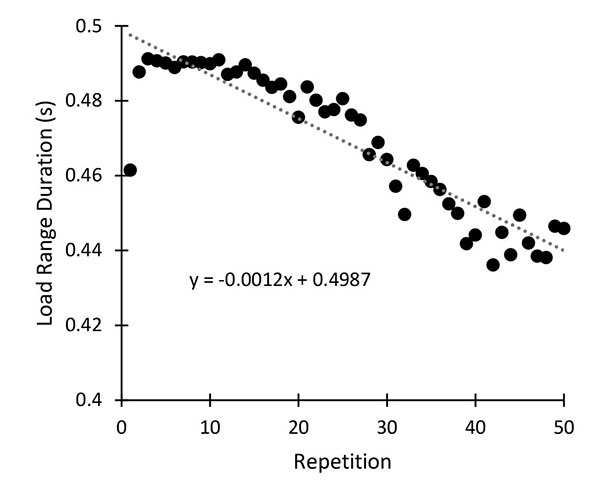
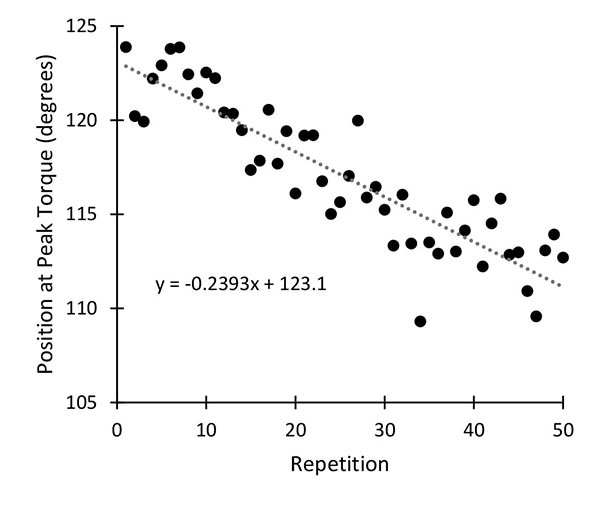
There was a significant inverse relationship between isokinetic load range duration (seconds) and repetition number (p<.001; mean + SD r=-..70±.17), where isokinetic load range decreased by approximately 12 percent across 50 repetitions. Fig. (1) shows the composite data from all subjects for the load range versus repetition number relationship with load range duration mean peak (.491 s) occurring at repetition three and mean minimum (.438 s) occurring at repetition 48. There was a significant inverse relationship between angle at PT and repetition number (p=.003; r=-.35±.35), where angle at PT decreased (closer to maximal flexion) by approximately 10° across 50 repetitions, with the latest (123.8°) mean PT occurring at the first repetition and earliest (109.3°) mean PT occurring at repetition 34. Fig. (2) shows the composite data from all subjects for the angle at PT versus repetition number relationship.

Fig. (1). A composite representation of the relationship between mean knee extension isokinetic load range duration and repetition number across 50 repetitions.
Fig. (2). A composite representation of the relationship between mean position at peak torque and repetition number across 50 isokinetic knee extension repetitions.

Fatigue Index

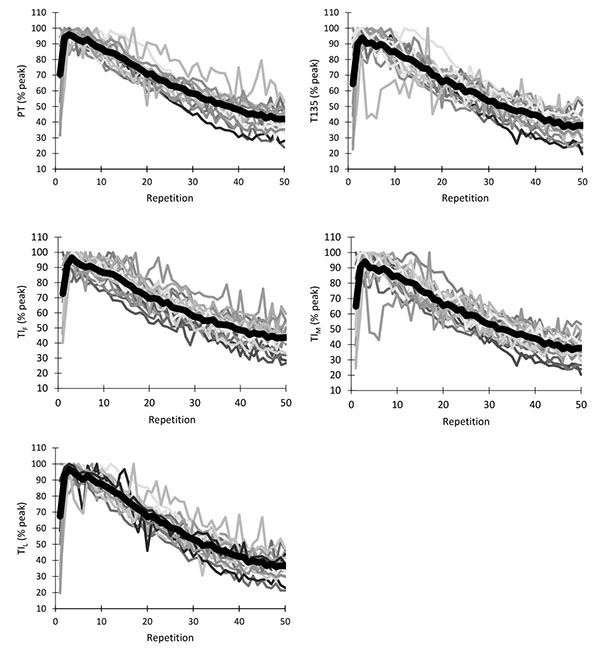
Individual torque curves can be viewed in Fig. (3). Fatigue Index means and SDs can be viewed in Tables (1 and 2). There was no significant three-way interaction between calculation method, repetition range and torque variable (p=.127; ƞ2=.114).

Fig. (3). Individual (thin lines) and mean (thick line) values across all isokinetic knee extension repetitions for peak torque (PT), torque at 135° (T135), torque integral over the full ROM (TIF), torque integral from 120°-150° (TIM), and torque integral over the load range (TIL).
Table 1.
Percent decline in torque output beginning from the repetitions with the highest torque outputs*.
Description Torque FI Mean FI SD
50 reps F3 TIF 49.19 12.12
PT 50.66 11.61
T135 53.48 12.7
TIM 54.13 12.57
TIL 56.51 10.95
30 reps F3 PT 30.57 11.61
TiF 30.96 13.07
T135 31.66 14.6
TIM 32.84 13.95
TIL 34.97 13.6
50 reps F5 TiF 50.68 10.34
PT 52.16 9.81
T135 55.56 10.58
TIM 55.87 10.47
TIL 58.2 9.19
30 reps F5 TiF 31.77 10.83
PT 31.85 9.01
T135 32.56 13.43
TIM 33.45 12.34
TIL 35.91 11.09
Table 2.
Percent decline in torque output beginning from the repetitions with the highest torque outputs*.
Description Torque FI Mean FI SD
50 reps P3 TiF 54.89 8.45
PT 56.53 8.11
T135 60.51 8.67
TIM 60.75 8.45
TIL 62.39 7.31
30 reps P3 TiF 38.59 8.03
PT 38.63 6.61
T135 41.89 8.08
TIM 42.41 7.26
TIL 43.74 7.39
50 reps P5 TiF 53.64 8.69
PT 55.17 8.45
T135 59.57 8.52
TIM 59.6 8.47
TIL 61.35 7.47
30 reps P5 TiF 35.82 8.31
PT 36.07 6.97
T135 38.63 9.76
TIM 38.99 9.43
TIL 40.71 8.07

There was a significant two-way interaction between repetition range and torque variable (p=.018; ƞ2=.208). When collapsed across calculation method, torque variable had a significant effect (ƞ2=0.324) on 30-repetition Fatigue Index and a significant effect (ƞ2=.650) on 50-repetition Fatigue Index (Fig. (4); note that * indicates a 95% confidence interval contained zero).

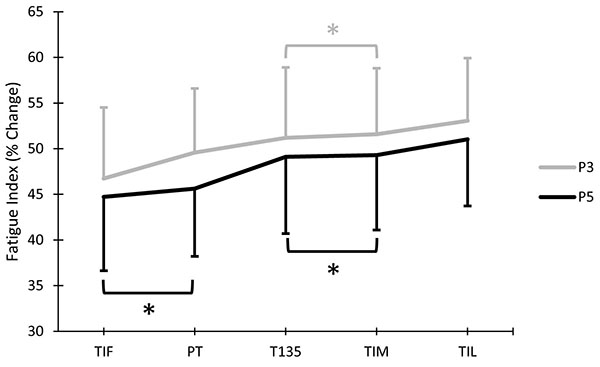
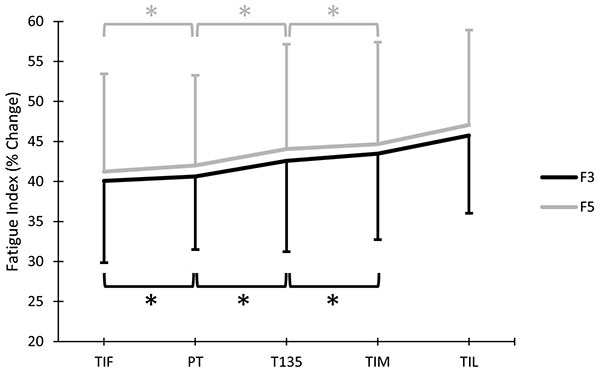
There was a significant two-way interaction between calculation method and torque variable (p=.026; ƞ2=.135). When collapsed across repetition range, torque variable had a significant effect (ƞ2=0.698) on P3 Fatigue Index and a significant effect (ƞ2=.658) on P5 Fatigue Index (Fig. 5). When collapsed across repetition range, torque variable had a significant effect (ƞ2=.406) on F3 Fatigue Index and a significant effect (ƞ2=.448) on F5 Fatigue Index (Fig. 6).

Fig. (4). The difference in isokinetic knee extension fatigue index between peak torque (PT), torque at 135° (T135), torque integral over the full ROM (TIF), torque integral from 120°-150° (TIM), and torque integral over the load range (TIL), collapsed across calculation methods, over the first 30 repetitions (ƞ2=0.324) and repetitions 1-50 (ƞ2=0.650). *Indicates no statistical difference (α=.05).
Fig. (5). The difference in isokinetic knee extension fatigue index of peak torque (PT), torque at 135° (T135), torque integral over the full ROM (TIF), torque integral from 120°-150° (TIM), and torque integral over the load range (TIL), collapsed across repetition range, using the peak three and last three repetitions (P3; ƞ2=0.698) and peak five and last five repetitions (P5; ƞ2=0.658). *Indicates no statistical difference (α=.05).
Fig. (6). The difference in isokinetic knee extension fatigue index of peak torque (PT), torque at 135° (T135), torque integral over the full ROM (TIF), torque integral from 120°-150° (TIM), and torque integral over the load range (TIL), collapsed across repetition range, using the first three and last three repetitions (F3; ƞ2=0.406) and first five and last five repetitions (F5; ƞ2=0.448). *Indicates no statistical difference (α=.05).

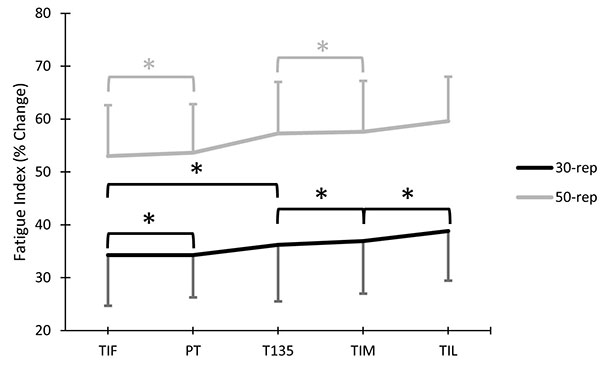
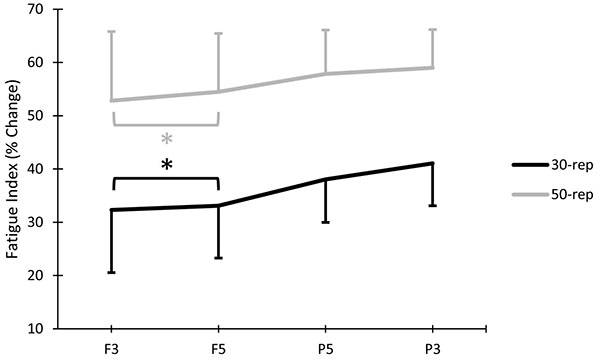
There was a significant two-way interaction between calculation method and repetition range (p<.001; ƞ2=.446). When collapsed across torque variables, calculation method had a significant effect (ƞ2=.444) on 30-repetition Fatigue Index and a significant effect (ƞ2=.442) on 50-repetition Fatigue Index Fig. (7).

Fig. (7). Isokinetic knee extension fatigue index using the first three and last three repetitions, the first five and last five repetitions, the peak three and last three repetitions, and peak five and last five repetitions, collapsed across torque variables, using repetitions 1-30 (ƞ=0.444) and repetitions 1-50 (ƞ=0.442). *Indicates no statistical difference (α=.05).

Torque Slopes

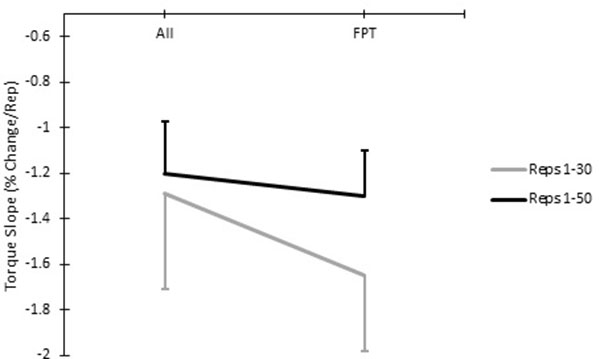
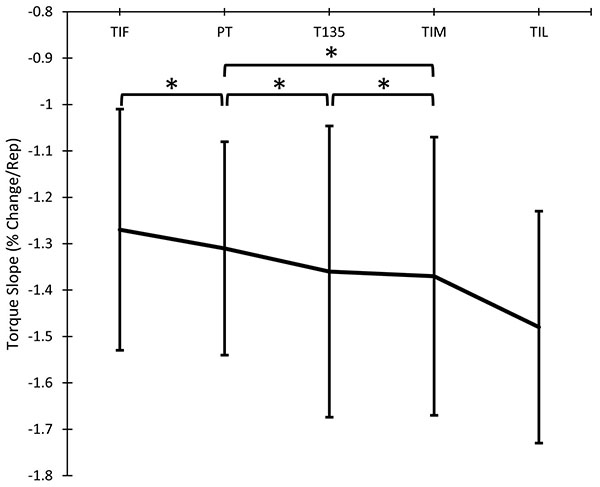
Torque slope means and SDs can be viewed in Table (3). For torque slopes, there was no significant three-way interaction between initial repetition position, repetition range, and torque variable (p=.445; ƞ2=0.046). There was no significant two-way interaction between repetition range and torque variable (p=.559; ƞ2=0.036). There was no significant two-way interaction between first repetition position and torque variable (p=.095; ƞ2=0.127). However, there was a significant two-way interaction between initial repetition position and repetition range (p<.001; ƞ2=0.609; see Fig. (8), spaghetti plots of individual responses are shown in Fig. (9). When collapsed across torque variables, for the 1-30 repetition range, FPT slopes (-1.65±.33) were more negative (p<.001) than slopes of all 50 repetitions (-1.29±.42). For repetitions 1-50, FPT slopes (-1.30±.20) were more negative (p=.001) than slopes that accounted for all repetitions (-1.20±.23). There was a large main effect of torque variable (p= <.001; ƞ2=.537) when collapsed across repetition range and first repetition position Fig. (10); spaghetti plots of individual responses are shown in (Fig. 11).

Fig. (8). Torque slopes, collapsed across torque variables, for repetitions 1-30 (p<.001) and repetitions 1-50 (p=.001), were more negative when all repetitions were used than when slopes excluded data that occurred before the repetition with the highest torque value (FPT).
Fig. (9). Individual subject torque slope values for repetitions 1-30 and repetitions 1-50, when all repetitions are included in the analysis and when slopes excluded data that occurred before the repetition with the highest torque value (FPT).
Fig. (10). Individual subject torque slope values for peak torque (PT), torque at 135° (T135), torque integral over the full ROM (TIF), torque integral from 120°-150° (TIM), and torque integral over the load range (TIL) collapsed across repetition range and initial repetition position. *Indicates no statistical difference (α=.05).
Fig. (11). Individual subject peak torque (PT), torque at 135° (T135), torque integral over the full ROM (TIF), torque integral from 120°-150° (TIM), and torque integral over the load range (TIL) slope values for each torque variable collapsed across repetition range and initial repetition position.

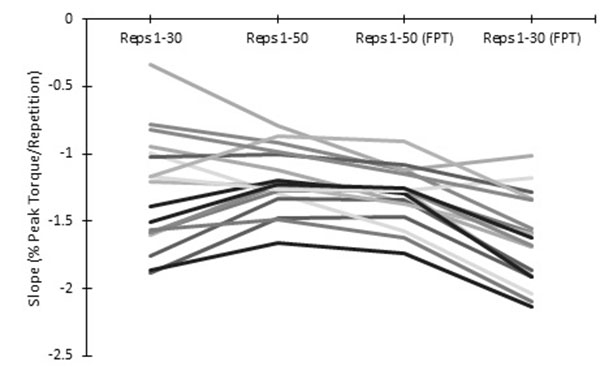
Relationship Between Torque and Repetition Number

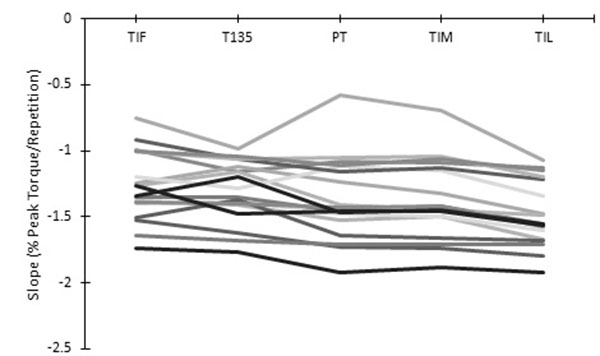
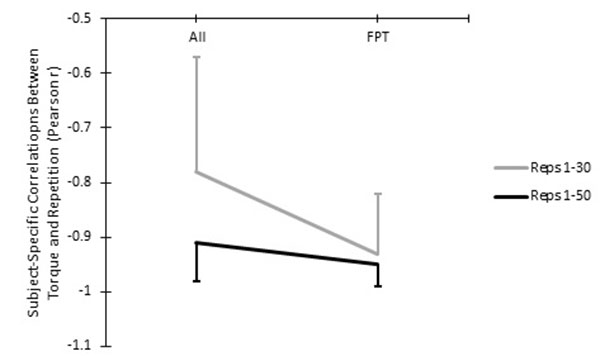
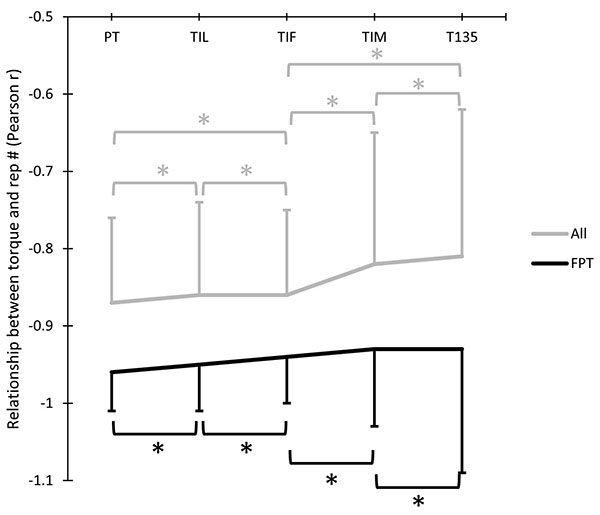
For the relationship between torque and repetition number (Pearson r values; Table (3), there was no significant three-way interaction between repetition range, initial repetition position, and torque variable (p=0.104; ƞ2=.126). There was no significant two-way interaction between repetition range and torque variable (p=.110; ƞ2=.115). However, there was a significant two-way interaction between initial repetition position and repetition range (p<.001; ƞ2=.639; see Fig. (12). When collapsed across torque variables, for repetitions 1-30, there were stronger linear relationships (p<.001) between torque and repetition number for FPT (-.93±.11) than when the analyses started at the first repetition (-.78±.21). When collapsed across torque variables, for repetitions 1-50, there was a more linear relationship (p=.002) between torque and repetition number for FPT (-.95±.04) than when all repetitions are considered (-.91±.07).

Fig. (12). Subject-specific linear correlations (mean + SD) between torque and repetition number (collapsed across torque variable); for repetitions 1-30 (p<.001) and repetitions 1-50 (p=.002) were more linear when all repetitions are included in the analysis and when slopes excluded data that occurred before the repetition with the highest torque value (FPT), than when all repetitions were utilized.

There was a significant two-way interaction between first repetition position and torque variable for Pearson r values (p=.038; ƞ2=.162). When collapsed across repetition range and all repetitions considered Fig. (13), there was a significant effect of torque variable (ƞ2=.302) and a significant effect of torque variable (ƞ2=0.336) on Pearson r values.

Fig. (13). The relationship between torque and repetition number for peak torque (PT), torque at 135° (T135), torque integral over the full ROM (TIF), torque integral from 120°-150° (TIM), and torque integral over the load range (TIL), collapsed across repetition range, using all repetitions (All; ƞ2=0.302) and using repetitions from the repetition where peak torque occurred (FPT; ƞ2=0.336).*Indicates no statistical difference (α=.05).
Table 3.
Slope and linearity of the torque change*.
Description Torque Slope Mean Slope SD r Mean r SD
50 Reps All Reps TIF -1.12 0.21 -0.92 0.05
PT -1.17 0.22 -0.93 0.06
T135 -1.2 0.27 -0.89 0.1
TIM -1.2 0.26 -0.9 0.09
TIL -1.31 0.21 -0.92 0.06
50 Reps FPT TIF -1.2 0.2 -0.95 0.03
PT -1.25 0.2 -0.96 0.04
TIM -1.32 0.22 -0.95 0.05
T135 -1.33 0.22 -0.95 0.06
TIL -1.42 0.19 -0.96 0.03
30 Reps All Reps TIF -1.23 0.39 -0.81 0.16
PT -1.24 0.34 -0.82 0.16
T135 -1.27 0.51 -0.73 0.27
TIM -1.29 0.48 -0.75 0.25
TIL -1.41 0.43 -0.8 0.19
30 Reps FPT TIF -1.54 0.37 -0.92 0.09
PT -1.57 0.28 -0.95 0.06
T135 -1.67 0.4 -0.91 0.17
TIM -1.67 0.38 -0.91 0.16
TIL -1.81 0.31 -0.95 0.09

DISCUSSION

The purpose of this study was an attempt to determine how methods of quantifying the fatigue-induced decline in torque production across repeated maximal effort isokinetic knee extension differ, and to determine which method(s) may be most appropriate. The main findings from this study are: 1) fatigue Index calculations differ between torque variables (see Figs. 4-6), 2) load range decreases as fatigue occurs (see Fig. 1), 3) the knee angle at which PT occurs systematically changes as fatigue occurs (see Fig. 2) and PT generally occurs before 130B0, 4) the use of initial repetitions underestimates fatigue, when compared to the use of repetitions occurring at and after the highest PT repetition (see Fig. 8), 5) there are stronger linear relationships between torque and repetition number when only repetitions occurring at and after the highest PT repetition are analyzed (see Fig. 12), and 6) PT, TIL and TIF have the strongest linear relationships between torque and repetition number (see Fig. 13).

We have shown that different methods to quantify torque can affect the absolute calculations of fatigue (Tables 1-3). Further, these measures of torque do not consistently affect the Fatigue Index calculations of every subject, as shown by the crossing of individual responses in Figs. (11 and 9). Thus, measuring different torque variables can affect the interpretation of data that includes repeated maximal effort isokinetic data. Brown, et al. [15, 16] have repeatedly shown that the beginning and end of every isokinetic dynamometer repetition contain positive and negative acceleration periods that result in movement periods at non-target velocities. This may make the use of the isokinetic load range torque interval an attractive option when analyzing repeated isokinetic contractions. However, load range decreases as repeated maximal effort isokinetic tests progress (Fig. 1), which has also been observed by Brown et al. [16]. This decrement in load range results in an overestimation of fatigue (Figs. 4-6), because even if torque did not decline across repetitions, less time under the same torque level would result in a lower torque integral. Some researchers have made an attempt to exclude the periods of positive and negative acceleration that occur at the beginning and end of every isokinetic repetition by measuring torque and EMG data over, approximately, the middle third of the ROM [1-4, 11, 17]. Unfortunately, PT can occur before the middle third ROM, which is common (Fig. 2). Thus, many researchers may not be capturing important data if they are only capturing the middle third ROM, which also suggests that capturing a single torque value at the middle of the ROM may be undesirable. To further complicate the issue, the most common measure utilized in Fatigue Index calculations, PT, occurs earlier in the repetition as the test progresses (Fig. 1). This means that when PT is utilized to calculate Fatigue Index across a 50 repetition test, the first three repetitions likely occur at a position that is approximately 10° different than the last three repetitions. Thus, an argument can be made that the only way to ensure that maximal strength or work is consistently captured across repeated isokinetic tests is to utilize the torque integral over the full ROM, even if it contains some non-isokinetic information. It should be noted that PT and full ROM torque integral typically result in similar results (Figs. 4-6 and 10). Importantly, these data suggest that researchers may benefit from the use of full ROM windows to relate measurements such as electromyographic and mechanomyographic signals to torque measures, where most have employed windows approximately equal to the middle third ROM [1-4, 11, 17]. Since this is the first study that has thoroughly analyzed the methodological differences between repeated isokinetic data, it is unknown what effect limb dominance or limb side may have on the measures analyzed in the current study. Furthermore, the current fatigue data is dependent upon each subject’s willingness to exert maximal effort through the entire test, which may be best indicated through the analysis of the EMG amplitude curve across the test. Although the data are not presented in the current study, the mean EMG amplitude curves of the vastus lateralis, vastus medialis, and rectus femoris did not exhibit considerable decrements in EMG amplitude across the 50-repetition test. Although these data suggest that voluntary activation did not change much throughout the test, it is impossible to know if subjects gave consistent submaximal effort throughout the test.

As has been shown previously [18], our spaghetti graphs of individual torque responses across 50 repetitions Fig. (3) show that, although each subject is fresh at the beginning of each test, initial repetitions do not accurately represent the peak strength or work capacity of nearly all the subjects. There may be a few possible explanations for this. This may be due, in part, to post-activation potentiation, which is plausible because potentiation is maximized when the conditioning muscle activation is greatest [28] and warm-up contractions are submaximal. A second influence may have been a progressive increase in muscle activation through the beginning of the test, which has been shown in previous studies [1, 4, 18, 29]. Another contributing factor may be due to the non-reciprocal nature of the first repetition of the test, which has been previously documented as having a much shorter load range window [16], in accordance with the current results (Fig. 1). Due to the low torque levels in the first few repetitions, the inclusion of such repetitions in the quantification of fatigue magnitude will result in the underestimation of fatigue (Fig. 7). Thus, instead of using F3 or F5, P3 or P5 should be used in Fatigue Index calculations. However, it should be noted that P3 will result in greater Fatigue Index values than P5 Fig. (7), but this difference is less when 50 repetitions are analyzed versus 30 repetitions. Importantly, when utilizing a strategy to exclude the low initial repetitions, decrements in torque through the first 30 repetitions have been shown to be highly correlated to the decrements in torque through 50 repetitions [30].

Similar to the quantification of fatigue using Fatigue Index, the inclusion of initial repetitions in the quantification of fatigue using the slope of torque across the test can lead to an underestimation of fatigue magnitude Fig. (8). Furthermore, the torque measurement used to quantify slope decrements differentially affects fatigue quantification between subjects as by the crossing of individual responses in Fig. (9). When utilizing a measurement of slope to interpret decrements in torque or work, the linearity of that relationship is of great importance. By including the first few repetitions in slope analyses, the linearity of the relationship between torque and repetition number is impaired Fig. (12). Although some articles have utilized all repetitions to quantify torque or work slopes [9, 24, 25], some researchers began their slope analyses from repetitions at which the highest PT or work occurred [22, 23], which seems to be the more appropriate method. However, this method introduces the issue of repeated effort tests having an unknown quantity of usable repetitions. Although it is not typically practiced, tests may include more than 50 repetitions, so the initial repetitions, which exhibit torque values less than the highest peak torque repetition, can be omitted and the 49 repetitions after the peak torque repetition can be included in the analysis of 50 repetitions.

CONCLUSION

In summary, there are many methodological considerations that researchers and practitioners should consider when collecting repeated maximal effort isokinetic data. These methodologic choices may impact how research is interpreted and how practitioners interpret athletes’ data. The torque integral over the full range of motion is likely the best representation of strength or work, as other measures may not capture the moment where maximal strength occurs or may systematically change across the duration of the test. Also, because measures of PT do not occur during the first few repetitions of a repeated maximal isokinetic test, when quantifying Fatigue Index, the peak three or peak five repetitions likely give a more accurate estimation of the decline in strength or work capacity. For similar reasons, when utilizing measures of torque or work slope to describe fatigue, researchers and practitioners should consider only analyzing repetitions that occur at and beyond the repetition at which the greatest torque value occurred.

LIST OF ABBREVIATIONS

PT = Peak torque
ROM = Range of motion
F = Full range of motion
M = Range of motion from 120°-150°
L = Range of motion at isokinetic target velocity
TIF = Torque integral over full range of motion
TIM = Torque integral over range of motion from 120°-150°
TIL = Torque integral over range of motion at isokinetic target velocity
F3 = Average of the torque values from the first three and last three repetitions
F5 = Average of the torque values from the first five and last five repetitions
P3 = Average of the torque values from the peak three and last three repetitions
P5 = Average of the torque values from the peak three and last five repetitions
FPT = Repetitions that occur at and beyond the repetition at which the greatest torque value occurred

ETHICS APPROVAL AND CONSENT TO PARTICIPATE

The study was reviewed and approved by The University of Kansas Human Subjects Committee.

HUMAN AND ANIMAL RIGHTS

Not applicable.

CONSENT FOR PUBLICATION

Written informed consent were obtained from all participant.

CONFLICT OF INTEREST

The authors confirm that this article content has no conflict of interest.

ACKNOWLEDGEMENTS

Declared none.

REFERENCES

1
Perry-Rana SR, Housh TJ, Johnson GO, Bull AJ, Berning JM, Cramer JT. MMG and EMG responses during fatiguing isokinetic muscle contractions at different velocities. Muscle Nerve 2002; 26(3): 367-73.
2
Ebersole KT, OConnor KM, Wier AP. Mechanomyographic and electromyographic responses to repeated concentric muscle actions of the quadriceps femoris. J Electromyogr Kinesiol 2006; 16(2): 149-57.
3
Cochrane KC, Coburn JW, Brown LE, Judelson DA. Effects of diverting activity on strength, electromyographic, and mechanomyographic signals. J Strength Cond Res 2014; 28(5): 1203-11.
4
Camic CL, Housh TJ, Zuniga JM, et al. Electromyographic and mechanomyographic responses across repeated maximal isometric and concentric muscle actions of the leg extensors. J Electromyogr Kinesiol 2013; 23(2): 342-8.
5
Larsson B, Karlsson S, Eriksson M, Gerdle B. Test-retest reliability of EMG and peak torque during repetitive maximum concentric knee extensions. J Electromyogr Kinesiol 2003; 13(3): 281-7.
6
Gerdle B, Larsson B, Karlsson S. Criterion validation of surface EMG variables as fatigue indicators using peak torque: a study of repetitive maximum isokinetic knee extensions. J Electromyogr Kinesiol 2000; 10(4): 225-32.
7
Thorstensson A, Karlsson J. Fatiguability and fibre composition of human skeletal muscle. Acta Physiol Scand 1976; 98(3): 318-22.
8
Stock MS, Beck TW, DeFreitas JM. Effects of diverting activities on Electromyographic amplitude and mean frequency. Kineziologija 2013; 45(2): 222-32.
9
Ivy JL, Sherman WM, Miller JM, Maxwell BD, Costill DL. Relationship between muscle QO2 and fatigue during repeated isokinetic contractions. J Appl Physiol 1982; 53(2): 470-4.
10
Weir JP, Keefe DA, Eaton JF, Augustine RT, Tobin DM. Effect of fatigue on hamstring coactivation during isokinetic knee extensions. Eur J Appl Physiol Occup Physiol 1998; 78(6): 555-9.
11
Mota JA, Stock MS, Carrillo EC, Olinghouse KD, Drusch AS, Thompson BJ. Influence of hamstring fatigue on the estimated percentage of fast-twitch muscle fibers for the vastus lateralis. J Strength Cond Res 2015; 29(12): 3509-16.
12
Beam W, Adams G. Exercise Physiology Laboratory Manual: McGraw-Hill. High Educ 2013.
13
Sangnier S, Tourny-Chollet C. Comparison of the decrease in strength between hamstrings and quadriceps during isokinetic fatigue testing in semiprofessional soccer players. Int J Sports Med 2007; 28(11): 952-7.
14
Ellenbecker TS, Roetert EP. Testing isokinetic muscular fatigue of shoulder internal and external rotation in elite junior tennis players. J Orthop Sports Phys Ther 1999; 29(5): 275-81.
15
Brown LE, Whitehurst M, Findley BW, Gilbert R, Buchalter DN. Isokinetic load range during shoulder rotation exercise in elite male junior tennis players. J Strength Cond Res 1995; 9(3): 160-4.
16
Brown LE, Whitehurst M, Findley BW, Gilbert R, Groo DR, Jimenez JA. Effect of repetitions and gender on acceleration range of motion during knee extension on an isokinetic device. J Strength Cond Res 1998; 12(4): 222-5.
17
Ebersole KT, Malek DM. Fatigue and the electromechanical efficiency of the vastus medialis and vastus lateralis muscles. J Athl Train 2008; 43(2): 152-6.
18
Wretling M-L, Henriksson-Larsén K. Mechanical output and electromyographic parameters in males and females during fatiguing knee-extensions. Int J Sports Med 1998; 19(6): 401-7.
19
Crenshaw AG, Gerdle B, Heiden M, Karlsson S, Fridén J. Intramuscular pressure and electromyographic responses of the vastus lateralis muscle during repeated maximal isokinetic knee extensions. Acta Physiol Scand 2000; 170(2): 119-26.
20
Fujita S, Mikesky A, Sato Y, Abe T. Fatigue characteristics during maximal concentric leg extension exercise with blood flow restriction. Int J KAATSU Train Res 2008; 3(2): 27-31.
21
Pincivero DM, Gear WS, Sterner RL. Assessment of the reliability of high-intensity quadriceps femoris muscle fatigue. Med Sci Sports Exerc 2001; 33(2): 334-8.
22
Maffiuletti NA, Bizzini M, Desbrosses K, Babault N, Munzinger U. Reliability of knee extension and flexion measurements using the Con-Trex isokinetic dynamometer. Clin Physiol Funct Imaging 2007; 27(6): 346-53.
23
Pincivero DM, Gandaio CM, Ito Y. Gender-specific knee extensor torque, flexor torque, and muscle fatigue responses during maximal effort contractions. Eur J Appl Physiol 2003; 89(2): 134-41.
24
Pincivero DM, Campy RM. The effects of rest interval length and training on quadriceps femoris muscle. Part I: knee extensor torque and muscle fatigue. J Sports Med Phys Fitness 2004; 44(2): 111-8.
25
Bosquet L, Gouadec K, Berryman N, Duclos C, Gremeaux V, Croisier J-L. Physiological interpretation of the slope during an isokinetic fatigue test. Int J Sports Med 2015; 36(8): 680-3.
26
Hinkle DE, Wiersma W, Jurs SG. Applied Statistics for the Behavioral Sciences 2003.
27
Vincent W, Weir J. Statistics in Kinesiology. Human Kinetics 1999.
28
Fukutani A, Hirata K, Miyamoto N, Kanehisa H, Yanai T, Kawakami Y. Effect of conditioning contraction intensity on postactivation potentiation is muscle dependent. J Electromyogr Kinesiol 2014; 24(2): 240-5.
29
Kellis E. The effects of fatigue on the resultant joint moment, agonist and antagonist electromyographic activity at different angles during dynamic knee extension efforts. J Electromyogr Kinesiol 1999; 9(3): 191-9.
30
McLeland KA, Ruas CV, Arevalo JA, Bagley JR, Ciccone AB, Brown LE, et al. Comparison of knee extension concentric fatigue between repetition ranges. Isokinet Exerc Sci 2016; 24(1): 33-8.