All published articles of this journal are available on ScienceDirect.
Modeling Judges’ Scores in Artistic Gymnastics
Abstract
Background:
In artistic gymnastics, performance is observed and evaluated by judges based on criteria defined in the code of points. However, there is a manifold of influences discussed in the literature that could potentially bias the judges’ evaluations in artistic gymnastics. In this context, several authors claim the necessity for alternative approaches to judging gymnastics utilizing biomechanical methods.
Objective:
The aim of this study was to develop and evaluate a model-based approach to judge gymnastics performance based on quantitative kinematic data of the performed skills.
Methods:
Four different model variants based on kinematic similarity calculated by a multivariate exploratory approach and the Recurrent Neural Network method were used to evaluate the relationship between the movement kinematics and the judges’ scores. The complete dataset consisted of movement kinematic data and judgment scores of a total of N = 173 trials of three different skills and routines from women’s artistic gymnastics.
Results:
The results exhibit a significant relationship between the predicted score and the actual score for six of the twelve model calculations. The different model variants yielded a different prediction performance in general across all skills and also in terms of the different skills. In particular, only the Recurrent Neural Network model exhibited significant correlation values between the actual and the predicted scores for all three investigated skills.
Conclusion:
The results were discussed in terms of the differences of the models as well as the various factors that might play a role in the evaluation process.
1. INTRODUCTION
In competitive sports, judgment of the performance is of vital importance. Sports performance can be either assessed by objective measurements (e.g., time in running, or points in tennis) or by subjective judgments (e.g. points in artistic gymnastics) [1]. In artistic gymnastics, performance is observed and evaluated by judges based on criteria defined in the code of points [2, 3]. Thereby, the assumption is, that highly skilled judges come to reliable and fair evaluations of observed performances [4, 5]. However, there is a manifold of potential influences discussed in the literature that could potentially bias the judges’ evaluations [6-9]. In this context, several authors claim the necessity for alternative approaches to gymnastics judging [10, 11]. A particular emphasis is laid on approaches utilizing biomechanical methods due to their high degree of measurement precision and reliability [12, 13]. In this context, one should acknowledge that also the International Gymnastics Federation is now strengthening the efforts to implement a complex judging support system based on movement data supporting the demand for an objective and potentially unbiased evaluation of gymnastics performance [14]. However, before implementing and road-testing a particular system, there has to be some empirical evaluation of such a system. Therefore, the aim of this study was to develop and evaluate a model-based approach for judging gymnastics performance based on quantitative kinematic data of the performed skills.
In sports where performance is assessed by objective measurement, such as time in running or points in tennis, there is an argumentation in the literature that there is no optimal movement pattern that is associated with high performance. Every expert has his/her own optimal movement pattern that fits the constraints in a given situation [15, 16]. In contrast, in artistic gymnastics particular movement characteristics have to be fulfilled. When judging artistic gymnastics performances during competition, the judgment is made based on criteria defined in the code of points to make the judgment as objective and comparable as possible. For instance, if a gymnast performs a skill with bent arms or bent knees, he/she may be punished with a deduction up to 0.50 points. If he/she touches the landing mat with one or two hands during landing, he/she may be punished with a deduction of 1.00 point. The final execution score is calculated by averaging three out of the five scores, whereby the highest and lowest scores are omitted from this calculation. This averaging procedure is thought to control for outliers [17].
Artistic gymnastics comprises fast and complex skills, and for the average person, it seems almost impossible to ascertain all movement-relevant information, which is necessary for a fair judgment and evaluation of the observed skill at hand according to the criteria defined in the code of points. Therefore, judges have to acquire particular knowledge as well as particular skills through specialized judging courses [18, 19]. It is well known that judgments of sports performance are influenced by many other variables than the mere performance, and are thereby often biased. Variables that influence the judgment process are social cognition, information processing, perception or memory processes [1]. For instance, it could be found that the evaluation by the gymnastic judges of the cross on the rings, which is a static strength element, is influenced by their viewing position. This might lead to biased evaluation scores, especially for floor routines where the skills are executed from different directions on the floor. While the viewing position is one source of judgment bias, there are many other sources in the environment of which people are even less aware of [20]. When it then comes to the encoding of the perceived information, prior knowledge may have an influence. For instance, novices may perceive a gymnastics floor routine as a random pattern of difficult movements, whereas for expert gymnasts, a gymnastics floor routine is the result of particular skills that should be performed in a prescribed way. Not only prior knowledge but also cues that evolve from the competitive environment itself are likely to influence performance judgments. For instance, it could be shown that serial position effects are involved when performances are judged in sequence [21, 22]. This may lead to the problem that the judgment of the presented performance may simply be influenced by the starting position of the gymnasts in a competition and thereby affect the competition outcome.
There is a strong argument in the relevant literature for biomechanically driven judging procedures, especially in technical sports such as gymnastics [10]. For instance, recently, a system capable of measuring horizontal displacement on the trampoline bed, together with the time of flight duration was presented [23]. The time of flight and horizontal displacement are two parameters that could potentially be useful in judging trampoline performance; however, movement technique consists of a considerable amount of other information that is not captured by these two parameters (i.e., changes in body posture during flight, amount of somersault and twist rotations, etc.). Another quite innovative approach using an algorithm was implemented in real-time computer vision software for rhythmic gymnastics [12]. This software extracted detailed velocity field information from body movements from video shots or live performance video streams of dance movements. By first analyzing the spatio-temporal trajectories and then comparing them with those stored in a database, the authors could reliably classify the recorded movement as well as calculate a judgement score. The method accurately determined scores for different standard gymnastic movements that were comparable to those determined by expert judges. However, this algorithm may work for simple movements but not for complex movements such as those found in gymnastics where static and dynamic skills in addition to twists and somersaults are performed in one routine. To capture all those different movement aspects, one needs complete kinematic information, which implies the capture of the performed movement with high accuracy in all three dimensions. Currently, software solutions exist that allow for a holistic and instantaneous data collection and analysis of kinematic information [24]. There is an expanse of other comprehensive research addressing the relationships between movement kinematics of gymnastics skill executions and judges` scores [25-31]. One common result of the aforementioned research was, that some kinematic variables correlated well with the judges’ scores. This is especially the case for the vault exercise, which is very fast, technical and with no artistic evaluation included [25]. There are several opportunities to investigate kinematics variables, from time-discrete values of selected variables to time and space continuous values of multiple variables. For example, investigating the skill of a handspring during the vault performance could be achieved by only analyzing the shoulder angle at the time when the gymnast first touches the vault after the first flight phase or by analyzing the interplay between the shoulder and the hip angle during the entire movement.
While the aforementioned approaches provide a strong argument for assessing biomechanical information in the evaluation of gymnastics skills, it might be questionable whether using time-discrete measures would be optimal here [32-34]. Futhermore, research highlights that the perception of motion is better when dynamic motion information is available compared to structural information alone [35, 36]. Thus, a biomechanical approach to gymnastics judging should capture the course of the skills to be judged with parameters that are perceivable by external observers, such as spectators who might have only sparse knowledge of biomechanics [37, 38].
In summary, when the evaluation of movement is based on the perception of movement, and the perception of movement is a holistic process that takes into account the kinematic pattern of the movement over time and space, then gymnastics skill performances with a similar kinematic pattern should be similarly compared to gymnastics skill performances with a different kinematic pattern. The aim of this study was to develop and evaluate a model-based approach to judge gymnastics performance based on quantitative kinematic data of the performed skills. Because the International Gymnastics Federation is strengthening the effort to implement a computer-based judging support system based on movement data, there is a demand for investigating this rationale. To identify the similarities and dissimilarities between the kinematic patterns of different movement realizations, two different methods were used, that is, a multivariate exploratory approach and a Recurrent Neural Network [39]. Four different model variants based on the two methods were used to prove a direct and positive relationship between movement kinematics and judges’ scores. Based on the previous findings, it was predicted that experts would evaluate gymnastics skills based on the kinematic patterns of a particular skill. More specifically, it is assumed, that two skill performances that are structurally identical in movement kinematics should be judged with the same score. The more two skill performances differ in movement kinematics, the more different the scoring should be.
2. MATERIALS AND METHODS
2.1. Description of the Dataset and Model Database
The complete dataset consisted of movement kinematic data and judgement scores of a total of N = 173 trials of three different skills from women’s artistic gymnastics (round-off – back handspring – back layout somersault on floor, n1 = 58; back handspring from handstand position on balance beam, n2 = 57; handspring on vault, n3 = 57; Note: Unfortunately, one trial had to be removed for the balance beam and vault due to problems with data collection). The number of trials was sufficient regarding an a-priori power analysis when expecting a medium effect (Cohens’ f = 0.25, type I error probability = .05, type II error probability =.20). The skills were performed by ten female high-level gymnasts (mean age: 11.50 ± 1.43 years). Every gymnast performed six to seven executions of each skill, which is similar to or even below their normal training workload. Gymnasts were active members of a national high-performance training center and they exhibited an average training amount of more than 25 hours per week. They participated at national and international competitions. All gymnasts were informed about the purpose of the study prior to data collection and participated voluntarily. The data collection took place after parental consent, and the study was conducted in line with the ethical guidelines of the local ethics committee, as well as in compliance with the Declaration of Helsinki for human research and the international principles governing research on humans. The task was for the participants to perform the aforementioned skills on each apparatus as they would do in a gymnastics competition. Thus, each apparatuses was set up in accordance with the competition guidelines of the International Gymnastics Federation for women’s artistic gymnastics [3]. Gymnasts’ performances were recorded by means of a digital video camera operating at 240 Hz (spatial resolution: 1920 x 1080 pixels). The camera was placed approcimately 15 meters away from the apparatus with its optical axis being orthogonal to the movement direction of the gymnast, simulating the judge’s perspective.
2.1.1. Judgment Scores
All 173 trials were presented to five subjects with high visual gymnastics expertise. All subjects were informed about the purpose of the study and gave their consent prior to data collection. They were asked to rate each of the trials on a visual analog scale that was anchored to six points according to the judgement guidelines of the German Gymnastics Federation for young gymnastics talents [40]. To evaluate the judgment scores, the inter-rater reliability was calculated (see Table 1). Finally, the judgment scores were averaged to give a final judgement score for each trial of the dataset [3].
2.1.2. Kinematic Data
The movement analysis software Simi Motion® [41] was used for digitizing and analyzing the movement kinematics of each of the trials. Thereby, a two-dimensional body model with the x and the y coordinates of the following body landmarks was determined: the forward section of the foot, ankle, knee, hip, shoulder, elbow, wrist, hand (in each case, right and left sides of the body) and head. The time-series of each digitized body landmark was time-normalized and rescaled to a time interval from zero to 1000; this was performed to ensure structural comparability between skills of (slightly) different duration. We calculated the angle time series denoting the x and y coordinates for the flexion and extension of both ankle joints, both knee joints, both hip joints, both shoulder joints, both elbow joints, both wrist joints as well as the orientation angle of the trunk. The free statistic software R [42] was used for further data processing and analysis. The neural networks were created using the Keras framework [43] in combination with tensorflow [44] to enable GPU training.
2.2. Model Assumptions and Calculations
To predict the judgment score from the gymnasts’ movement kinematic data, an approach based on the structural similarity of the movement pattern was used. The approach implied a direct and positive relationship between the movement kinematics and the judges’ scores. Thus, one of the main assumptions was that two skill performances that are structurally identical in movement kinematics should be judged with the same score The more two skill performances differ in movement kinematics, the more different the scoring should be (Fig. 1).
2.2.1. Structural Similarity
Structural similarity was operationalized using the Euclidean distance or a specific pattern in the neural network. Euclidean distances are a mathematical measure, representing the mathematical distance or similarity between two objects. To get the Euclidean distances, cumulated squared differences were calculated for a particular choice of corresponding joint angle time-series between two trials [45]. An eight-segment model of the human body with the corresponding knee joints, hip joints, shoulder joints (in each case, right and left sides), as well as the orientation angle of the trunk were used [46, 47]. Therefore, one skill performance contained information from eight variables. The calculated squared differences were summed to give a final Euclidean distance value. A smaller Euclidean distance between two skills indicated a higher degree of kinematic similarity between the two skills, whereas a larger Euclidean distance between two skills indicated a lower degree of kinematic similarity of the two skills. The calculation of the Euclidean distances resulted in one distance matrix for each apparatus.
The Recurrent Neural Network is a specific form of an artificial neural network [48]. The network was trained to imitate the judges’ scoring. Neural networks are a form of machine learning, of which the architecture of the model is roughly based on the human brain. The model consists of inputs and outputs, which are connected by so-called axons and neurons. Similar to the human nervous system, a neuron fires when a specific amount of energy has reached it and by firing, a signal is passed to one or more other neurons. In an artificial neural network, neurons are represented by nodes in a layer and the signals are passed via so-called weights. Information is given to the network in the form of numerical values. These values are passed through the network using the weights and neurons. The output of the network is a numerical form as well, which means that these values have to be interpreted depending on the use case.
For the given use case, the network was given the joint angles of the body as well as the absolute position of the joints in the video frame. The data were inputted sequentially into the network. The joint angles were normalized using a sine function. This created two advantages: first, the data were in a fixed range of -1 to 1, and second, the data kept numerically distant values close, such as the angles 359° and 1°. The target values of the judges’ scores were normalized to values between 0 and 1 by dividing them by 100. A GRU was used as an RNN layer type [49]. judgments and removing the best and the worst, to taking only the kinematic pattern. This resulted in the following five model variants: 1.) Model variant #1 “best/worst”: We selected the two trials from the database with the best and the worst final judgment score. The predicted score of a particular evaluation trial was calculated as the weighted average from the best and worst scores, thereby using the Euclidean distances between the evaluation trial and the best/worst trials as the weights for the calculation. 2.) Model variant #2 “nearest neighbor”: The database trial with the lowest Euclidean distance to the evaluation trial (i.e., the greatest similarity between both trials in terms of movement kinematics) defined the score of the evaluation. 3.) Model variant #3 “three out of five neighbors”: Three final judgment scores of the five most similar database trials (compared to the evaluation trial in terms of movement kinematics) were averaged to give the score for the evaluation trial. Thereby, the highest and lowest final judgment scores were omitted from this calculation. 4.) Model variant #4 “recurrent neural network”: The information about the specific pattern of the neural network concerning the kinematics data was used as input.
2.2.2. Model Variants
On the basis of these approaches, five different model variants were developed to simulate the judging process. With the five models, the bandwidth of possibilities of judging was covered, from taking the order of the judgments to taking five
2.2.3. Model Prediction
For the training and evaluation trials, n = 20 trials for each skill were randomly selected to get an amount of approximately two-thirds for the model’s database and an amount of approximately one-third for the training database Table 1. We needed to ensure that the database trials and evaluation trials did not differ in average scoring and were thus suitable for prediction modeling. Therefore, the mean scores of the database trials were compared to the mean scores of the evaluation trials by calculating the Wilcoxon rank-sum test because of their non-normal distribution. For the model variant #4 “recurrent neural network”, the training was as follows: The weights of the networks were initialized randomly, and thus, the output of the network was useless in the beginning. The weights were adjusted to give better outputs. The adjustment was performed using an algorithm called the backpropagation algorithm. When using backpropagation, an error was calculated at the output layer, whereas that error was the difference between the values the network created and the values the network should have created. Using that error and the targets, the change in the weights was calculated such that the output approached the desired values.
To estimate the prediction performance of each model variant, we calculated Spearman’s rank correlation coefficients between the predicted and original scores of the evaluation trials for all model variants and all apparatuses [50].
3. RESULTS
The Shapiro-Wilk test of normality was used to investigate whether the judgment scores (predicted and original scores) were approximately normally distributed. Most of the scores were non normally distributed. Therefore, the Wilcoxon rank-sum test was used, to ensure that the database trials and evaluation trials did not differ in average scoring and revealed no significant differences between scores for any of the three apparatuses. Table 1 presents the mean original scores of the database trials and evaluation trials for the three apparatuses as well as the results of the Wilcoxon rank-sum test.
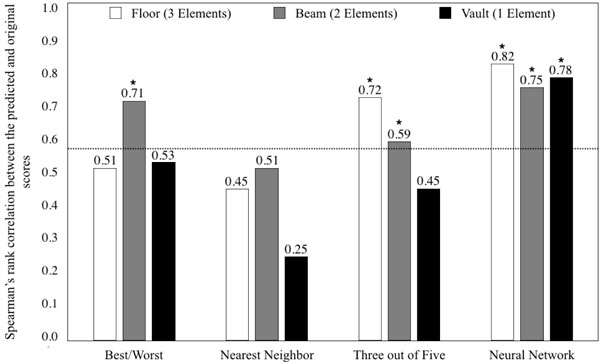
The prediction performance of each model variant was estimated by calculating the Spearman’s rank correlation coefficients between the predicted scores for the model and the original scores from the judges for each of the three gymnastics skills. The significance level was defined a priori as 5%. A one-tailed bivariate correlation with N = 20 cases a type-I error probability of .05 and a Bonferroni correction could be calculated with a value of rcrit = .57. Thus, for a correlation coefficient to become statistically significant, its value had to be larger than rcrit.(Fig. (2)). In addition, the predicted mean scores of all evaluations were calculated and compared to the original mean scores of all evaluation trials using the Wilcoxon rank-sum test; this was done for all model variants and all apparatuses (Table 2). Fig. (2) presents the calculated Spearman’s rank-sum correlation coefficients per model variant and per apparatus. Table 2 highlights the mean original scores of the judges for the evaluation trials as well as the mean scores of the evaluation trials which were predicted by the different model variants.
First, six out of twelve correlation coefficients reached statistical significance with regard to a critical r value of .57 (with a Bonferroni corrected p < .004), thereby indicating a significant relationship between the predicted scores and original scores of the evaluation trials (Fig. 2). Only the model variant #4 “recurrent neural network” exhibited a significant relationship between the predicted and original scores for all apparatuses: floor, rs(56) = 0.82, p < .001; beam, rs(49) = 0.75, p < .001; and vault, rs(56) =, 0.78, p < .001. The model variant #2 “nearest neighbor” did not exhibit a significant relationship between the predicted and original scores for any of the apparatuses: floor, rs(20) = 0.45, p .< .044; beam, rs(20) = 0.51, p < .023; and vault, rs(20) = 0.25, p < .292. The model variant #1“best/worst” only showed a significant relationship for the beam, rs(20) = 0.71, p < .001, whereas the results were not significant for the floor, rs(20) = 0.51, p = .021, and the vault, rs(20) = 0.53, p = .016. For the model variant #3 “three out of five neighbors”, only the floor, rs(20) = 0.72, p < .001, and beam, rs(20) = 0.59, p = .003, showed a significant correlation, whereas the correlations for the vault, rs(20) = 0.45, p = .48, was not significant.
4. DISCUSSION
The aim of this study was to develop and evaluate a model-based approach to judge gymnastics performance based on quantitative kinematic data of the performed skills. Four different model variants were compiled to predict the judgment scores on the basis of the kinematic information. The results showed a significant relationship between the predicted scores and the original scores for six of the twelve gymnastic skill - model combinations. The different model variants yielded different prediction performances in general overall skills and also in terms of the different skills. It was assumed that gymnastics skill performances with similar kinematic patterns reveal similar evaluation scores. Similarity is thereby defined in terms of the information about the time courses of the main body angles. These are important characteristics because they describe gymnastics skills in a holistic way, and other kinematic characteristics can easily be computed from these values [34]. Our approach is similar to the approach of Diaz-Pereira et al. [12]. who assessed velocity covariance trajectories instead of the angle values. The authors showed that that the covariant velocity trajectories contain information about the spatio-temporal aspects of a particular motion to extract the quality differences between movements. However, this algorithm may work for simple movements but not for complex movements such as those found in gymnastics where static and dynamic skills in addition to twists and somersaults alternate. By taking time-courses of the body landmarks as well as the resulting angle courses, the approach describes another tool that is capable of recognizing and scoring the movement quality of complex gymnastic skills.
| Apparatus | Database Trials | Evaluation Trials | ICCall |
Mean Score of Database Trials |
Mean Score of Evaluation Trials |
Z | p |
|---|---|---|---|---|---|---|---|
| Floor | 38 | 20 | 0.75 | 3.94 ± 1.90 | 3.99 ± 1.99 | 0.08 | .818 |
| Balance Beam | 37 | 20 | 0.85 | 3.94 ± 2.23 | 3.52 ± 2.31 | 1.24 | .216 |
| Vault | 37 | 20 | 0.83 | 3.35 ± 1.90 | 3.42 ± 1.81 | 0.23 | .933 |
| Model Variant | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Appa-ratus | Best/ Worst | Z | p | Nearest Neighbor | Z | p | Three out of Five | Z | p | Recurrent Neural Network | Z | p |
| Floor | 3.73 ± 1.22 | 1.47 | .140 | 3.46 ± 1.75 | 1.85 | .063 | 3.84 ± 1.69 | 0.34 | .735 | 3.70 ± 0.79 | 2.18 | .029* |
| Beam | 3.87 ± 2.38 | 0.85 | .394 | 3.65 ± 2.13 | 0.31 | .756 | 3.91 ± 2.11 | 0.89 | .372 | 4.30 ± 1.00 | 0.86 | .390 |
| Vault | 3.30 ± 2.10 | 0.06 | .947 | 3.34 ± 1.89 | 0.07 | .946 | 3.53 ± 1.75 | 0.39 | .695 | 3.10 ± 1.11 | 1.88 | .060 |
It is assumed that the kinematic pattern of a gymnastics skill contains the relevant information for an accurate performance judgment [36]. Several researchers illustrated that judges make their evaluation not only on the basis of kinematic similarity but also by taking some more subtle features into account that are not directly captured via movement kinematics [51, 52]. Those subtle features may lead to bias in the judgment process because their perception and encoding may be influenced by social cognition, information processing or memory processes [1]. These assumptions lead to the idea of making the judgment in artistic gymnastics more objective by using technical methodologies that predict judgment scores on the basis of kinematic variables. The study is the first approach in this direction and offers interesting results.
There are several aspects of the results that should be discussed in terms of this assumption. Prediction models that take into account only one trial Model variant #2 “nearest neighbor”, two trials Model variant #1 “best/worst” or five trials Model variant #3 “three out of five neighbors” were less accurate in their score prediction than the neural network approach. This was particularly the case for the gymnastics movement handspring on the vault, which has a rather short duration. This result may be explained by two points. First, because of the short duration of the skill, the time to receive the relevant kinematic movement information is limited, whereas the observer has more time available for a routine during the floor exercise, which incorporates three gymnastics skills in a row. Secondly, because the vault always comprises one element, the complexity and velocity of the movement are higher than for the other elements, which also could lead to less accurate results. Because of the demands of the vault, in general, this apparatus should be first to benefit from a kinematic assessment compared to other apparatuses. It could be interesting to compare the kinematic computer-based judgment results with the judgment results of gymnastics experts acquired from slow-motion videos.
The prediction performance was, in general, the best for the neural network model. The trials where the network gave a different score than the majority of the judges was interesting at this point. An indicator that a neural network has started learning and has understood the given data is that it does not just give the same score for every test input but gives high scores for the same scores where the judges gave high scores as well and gives low scores for other trials accordingly. This could mean that the network is being more objective and thus comes to a different conclusion compared to that of the judges. Assuming that the scores from the network are accurate, an interesting use case comes to mind. Since the network can basically create scores instantly, it could be embedded in a program that is filming gymnasts and then immediately gives feedback after the scores are assigned where the kinematics variables should be changed. Thus, the approach could be applied in competition, perhaps not as an alternative approach for a human evaluation but for complementing the actual scoring procedure. The recording and digitizing of the performance were performed using a semiautomatic system. There are hardware options available that are more precise in their tracking of the relevant kinematic features, release a higher amount of kinematics variables and are much faster in their digitizing process. For instance, there is direct three-dimensional silhouette tracking software available that extracts movement kinematics of the human body by means of a high-performance silhouette tracking algorithms [24].
Another advantage is, that the approach can be easily applied to data from different motion capture systems because the algorithm can be adapted to various kinematic variables. By having a larger dataset and different kinematic variables, one could compare a larger number of different models and thereby find the most precise one. This leads us to the limitation of the study where one specific aspect should be highlighted. First, two of the models were a combined reference-based and nearest-neighbor averaging approach or an only reference-based approach. By taking into account not only the kinematic information but also the scoring information for the model approaches, one uses the scoring information to predict the score. By labeling the kinematic information as a stable factor and the scoring information as a variable (changeable through different raters) factor that contains human bias, the model approaches differ in their independence of the human evaluation bias. The variability of the variable factor changes and should increase by a larger number of trials and scores per trial. The better prediction of the prediction model neural network could thereby arise from the large number of trials in the model but also from the lower bias originating from the variable factor.
Furthermore, it would be interesting to investigate not only whether models containing different variables and a different number of variables tracked from different motion capture systems leads to a different score predictions but also which variables are most precise in predicting the score. For example, if a model that takes into account only the hip angle would lead to the same results as a model taking into account four or five time courses of body angles, but this is not the case for a model on the basis of the knee angle, then it might be assumed that the hip angle is more relevant for evaluating gymnastics skills than the knee angle. Additionally, the approach should be tested by taking three-dimensional instead of two-dimensional kinematics data and by testing the models with data of skill realizations at a broader base of expertise level and skills that improve the procedure of achieving the judgment scores.
One factor that should always be kept in mind when dealing with computer-based methodologies is the psychological aspects of judging human behavior. It could be assumed that being judged by a computer or a human being leads to behavioral differences in skill execution. It may be assumed that each performance has a certain emotional expression that could hardly be captured by computer-based technologies. On the other hand, there is the question of trust in computer-based technologies and their error rate. They are more objective than human beings, but there are many aspects of motion capturing or of the algorithm that could lead to errors.
CONCLUSION
Overall, the approach utilized in this study to predict the evaluation scores of different gymnastics skills using a combined reference-based and nearest-neighbor averaging approach is a novel and important topic as the FIG is attempting to implement a judging support system based on move ment data. The study revealed the first interesting results that offer practical applications as well as further research questions to complement the judging procedure in gymnastics competition or similar sports areas with technical methodologies.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
The study was approved by the Institutional Review Board of Leipzig University.
HUMAN AND ANIMAL RIGHTS
No animals were used for this study. All humans research procedures performed in the current study were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
CONSENT FOR PUBLICATION
All participants were informed about the protocol and gave their written informed consent before participating in the study.
CONFLICT OF INTEREST
There are no conflicts of interest to declare.
FUNDING
The study is part of a PhD project and was funded by the scholarship “Doktorandenförderplatz” (PhD scholarship) of Leipzig University.
ACKNOWLEDGEMENTS
Declared none.


