All published articles of this journal are available on ScienceDirect.
Numerical Study of Non-Newtonian Blood Behavior in the Abdominal Aortic Bifurcation of a Patient-Specific at Rest
Abstract
Background:
The interaction of blood flow with walls of blood vessels is central for the development and maintenance of cardiovascular health. The analysis of wall shear stress is, therefore, fundamental in hemodynamic studies.
Objective:
The aim of this work is to study numerically the influence of the shear thinning blood properties on the hemodynamics in the abdominal aortic bifurcation for a patient-specific at rest.
Methods:
Were tested two models for the blood dynamic viscosity, one Newtonian and other non-Newtonian, with dependence on hematocrit and total protein minus albumin.
Results and Conclusion:
The results show the shear thinning behavior influence on the velocity distribution and wall shear stress. Furthermore, wall shear stress values are globally lower for non-Newtonian blood model at high velocity values than those for the Newtonian blood model. However, for low velocity values this behavior is inverted.
1. INTRODUCTION
Wall shear stress (WSS) is a very important quantity in studies of hemodynamic in the cardiovascular system. Several biomechanics works have highlighted the particular hemodynamics occurring within the cardiovascular system. The relationship between wall shear stresses and the sites where atherosclerosis develops has motivated much of the research on arterial hemodynamics in the last decades. It is now well accepted that blood flow on the walls of the cardiovascular system are central to the development and maintenance of cardiovascular health and the arterial sites most vulnerable to the atherosclerosis exhibit low wall shear stresses or, a change of WSS rapidly in time or space. These conditions are likely to prevail at places where the vessel is curved; bifurcates; has a junction, a side branch, or other sudden change in flow geometry; and when the flow is unsteady [1, 2].
Shear stress evolution in stenosis vessel can be correlated with the complex rheology of the blood which can explains the decrease of the internal vessel diameter in time, wall shear stress play an important role in remodeling the arterial wall and can lead to arterial thickening [3]. On the other hand, the problem of non-Newtonian and nonlinear blood flow through a stenosed artery was studied numerically where the non-Newtonian rheology of the flowing blood is characterised by the viscosity Power-law model [4]. More recently Deplano et al. [5] developed a unique in vitro set-up to analyse the influence of the shear thinning fluid properties on the flow dynamics within the bulge of an abdominal aortic aneurysm.
Furthermore several studies show some correlation between exercise training and WSS developed in cardiovascular system. For instance, exercise training is a well-established and potent physiological stimulus that reduces cardiovascular events [6]. The cardio protective effects of exercise training may, at least in part, be explained by the direct effects of repeated exercise bouts on the vasculature [7]. Indeed, exercise training improves vascular function, which relates to decreased cardiovascular risk and attenuation of atherogenic processes. In addition, exercise training decreases artery wall thickness [8, 9], which may be associated with a decreased progression of atherosclerosis. Others studies also demonstrate the importance of episodic increases in local shear stress to increase conduit artery diameter, and observational data suggest an inverse correlation between resting shear stress and carotid artery wall thickness [10].
In this work, we present a first study of the hemodynamics in the bifurcation of abdominal aorta for a patient-specific in rest that will be completed in future with new outcomes for the same patient when subjected to exercise training. Two blood viscosity models, Newtonian and non-Newtonian (Walburn-Schneck’s model), were compared in a realistic simulation of blood flow in the bifurcation of the abdominal aorta. The anatomic geometrical model was obtained by 3D reconstruction from Computed Tomography 2D images and hemodynamic parameters values were obtained from blood tests and by Doppler ultrasonography in a healthy adult in rest. In this study, it is assumed blood as an incompressible fluid, with laminar flow in a transient regime and rigid vessel wall. The finite volume method was used to study the velocity and WSS distributions during a heartbeat and hence identify relationships between them.
2. METHODS
2.1. Governing Equations
In the present paper the hemodynamics is assumed to be laminar and pulsatile during a full cardiac cycle. The values of Reynolds number are always less than 2300 in the whole extension of the studied artery. The governing equations are the incompressible Navier–Stokes equations and are given by the conservation mass equation
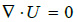 |
(1) |
and by the conservation of momentum equation
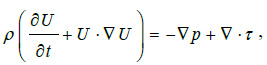 |
(2) |
where U is the fluid velocity vector, ρ the blood density and p the static pressure. τ is the stress tensor which is linearly dependent on the rate of deformation tensor D. With τ = 2η(γ)D, where D=(
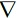 U +
U +
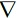 UT) ⁄ 2, η is the viscosity of the blood and γ is the shear rate.
UT) ⁄ 2, η is the viscosity of the blood and γ is the shear rate.
Were considered two models for the patient blood viscosity; one Newtonian and other non-Newtonian. The Newtonian viscosity is given by the Einstein equation [11] for the viscosity,
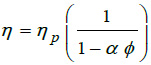 |
(3a) |
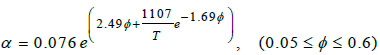 |
(3b) |
where T is the temperature in kelvin, ϕ the hematocrits concentration and ηp is the plasm viscosity. For our patient ϕ =0.375 at T= 310 K, then from equations (3) the Newtonian viscosity is 0.002393 Pas. For non-Newtonian viscosity was used the Walburn-Schneck’s model [12], given by.
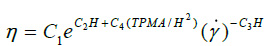 |
(4) |
The parameters used in the equation (4) to estimate the non-Newtonian viscosity were C1=0.000797, C2=0.0608, C3=0.00499, C4=14.585, H=37.5%, TPMA =66g/1 is the Total concentration Protein Minus Albumin and H is the hematocrit obtained from the blood tests performed to the patient participating in this study [13]. This model is applied to predict the non-Newtonian behavior and is compared with the Newtonian model, equation (3).
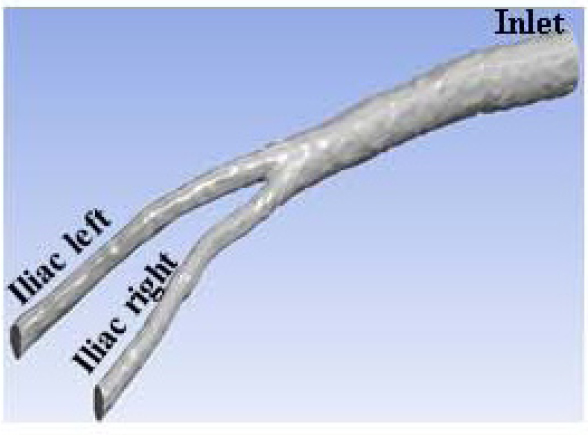
Fig. (1) shows the 3D geometry of the bifurcation of abdominal aorta artery for the patient-specific used in the present study. The 3D model was built with software Inventor 2015 from the CT imagens of the patient.
2.2. Boundary Conditions
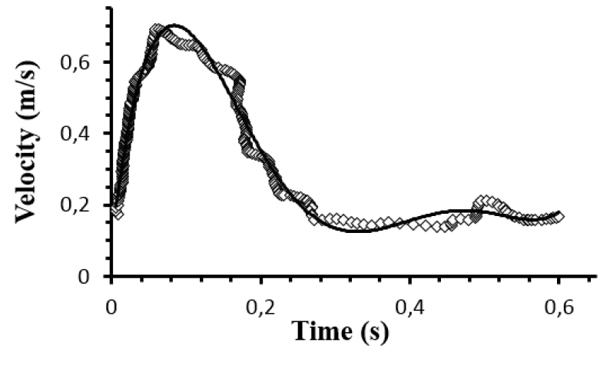
The velocity distribution at the inlet boundary (z = 0) was obtained by Doppler ultrasonography. Fig. (2) shows the inlet profile velocity during a cardiac cycle with period T = 0.63s, which correspond to the heartbeat rate of 95 beats per minute. For blood density was considered the value of 1050 kg/m3. At the iliac outlets, the Fluent outflow condition was imposed with 50% of the flow in each of the iliac arteries. Furthermore, the aortic walls were assumed rigid and no slip condition was applied.
2.3. Numerical Methods
The finite volume method was used as previously described [13-17] to study the velocity and WSS distributions during a cardiac cycle. The governing equations were solved with software Fluent employing a second-order upwind scheme, whereas the SIMPLE algorithm was employed to couple the pressure and velocity fields. The inlet boundary condition was implemented using a simple user-defined function. Was used a time-step size 50 times smaller than the period of the heartbeat. The convergence criteria were considered to be satisfied when the residuals of the continuity and momentum equations reach levels, for both, less than 10-6.
To test if the mesh is sufficiently refined to produce the required accuracy some simulations were carried out for three different meshes with about of 130000, 250000 and 320000 nodes. The difference between the solutions obtained for governing equations with the three aforementioned meshes were always less than 3-4%. Then, the mesh of ~130000 nodes was considered sufficient to the objectives of the present study. In addition to the numerical accuracy check, the numerical simulations were validated by matching with experimental data of velocity profiles at the iliac outlets, acquired by Doppler ultrasonography.
3. RESULTS
Computational fluid dynamics was performed using medical information for a specific patient. The 3D model for the abdominal bifurcation was reconstructed from imaging data obtained from Computed Tomography. The specific patient geometry combined with realistic boundary conditions withdrawals from medical information is essential to capture the complexity of the hemodynamics, offering promising approaches to advance personalized medicine in clinical assessment and diagnosis. On the other hand, the shear thinning behavior of the non-Newtonian blood viscosity is captured by using the Walburn-Schneck’s model given by equation (4).
Fig. (3) shows, for the Newtonian case, the velocity distributions in different cross sections of the abdominal bifurcation for t = 0.048s and t = 0.084s. The velocity distribution in each cross section shows that higher magnitudes of the velocities occur in the right iliac during the systolic peak as consequence of the smaller area of the cross sections in the right iliac and due to its tortuosity.
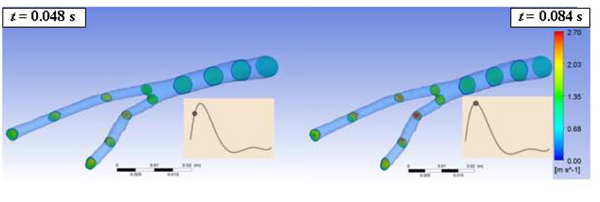
Fig. (4) shows the average velocity throughout the abdominal bifurcation at t = 0.048s and t = 0.084s of a cardiac cycle. In both cases, Newtonian and non-Newtonian viscosities, the higher velocity occurs in right iliac. The lines represent the velocity for the Newtonian and non-Newtonian blood viscosities. Note that the average velocities are de same in both cases as a consequence of the mass conservation (eq.1).
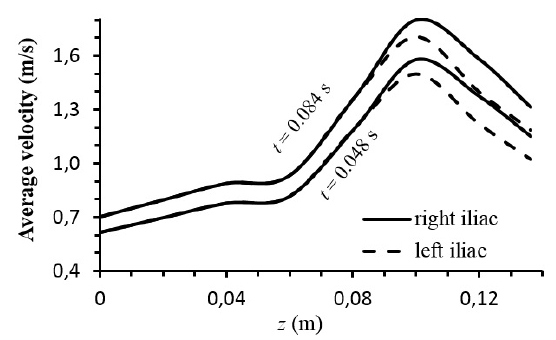
Fig. (5) shows the distribution of the wall shear stress (WSS) throughout the abdominal bifurcation at t = 0.084s and t = 0.6s in a cardiac cycle. In both cases the higher values of WSS occur on the aortic bifurcation. On the other hand, for t = 0.084s which corresponds to the maximum value of the velocity, the higher values of WSS extend from bifurcation to the iliac arteries however the non-Newtonian case presents highest values than the Newtonian case.
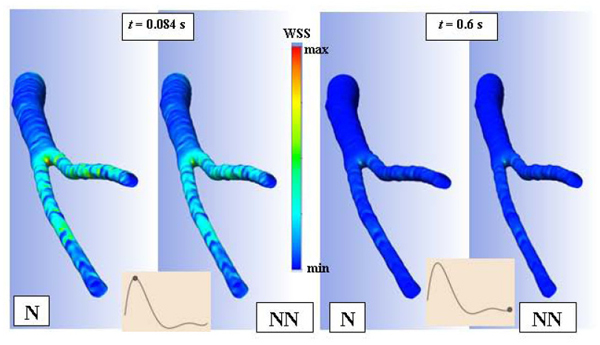
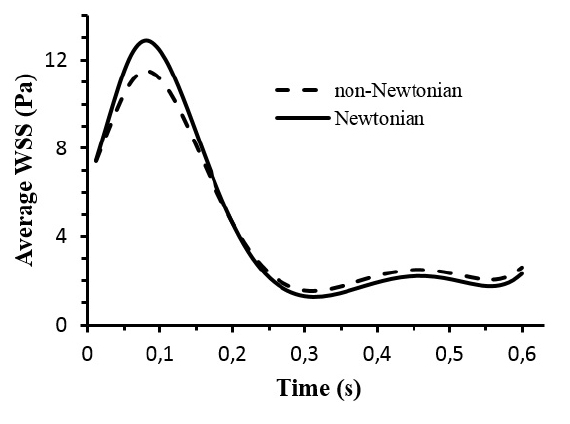
Fig. (6) shows the average WSS throughout the abdominal bifurcation at t = 0.084s corresponding to the systolic peak and at t = 0.6s corresponding to an instant at the end of diastole. For t < 0.2s the average WSS values are smaller for the case of the non-Newtonian viscous flow. For t > 0.2s the aforementioned behavior is reversed, that is, the average WSS values are smaller for Newtonian viscous flow. These behaviors are attributed to the blood viscosity models. For the Newtonian model the blood viscosity is constant whereas the non-Newtonian blood viscosity is dependent on the blood shear rate.
4. DISCUSSION
The application of computational fluid dynamics to the investigation of the hemodynamic in the cardiovascular system cannot be dissociated of some assumptions. In general the CFD assumptions are related with the data set limitations such as viscosity models, specific flow or geometry details because are not precisely known. In this work the influence of different models of viscosity were investigated with CFD. We found that the model of viscosity have impact in the hemodynamic. The average velocity distribution is not affected by the viscosity model (Fig. 4). For WSS distribution the non-Newtonian effects are more pronounced in the iliac arteries due to the tortuosity of the patient anatomy (Fig. 5). Furthermore the non-Newtonian viscosity has a shear thinning behaviour, that is, the blood viscosity is a decreasing function of the shear rate (eq. 4). At low shear rate, the viscosity increases, while for high shear rate the viscosity decreases. During the systole the blood flow is subjected to higher flow rate and consequently the shear rate is higher near of the artery wall. In its turn the viscosity decreases resulting, in general, in a decrease in WSS relatively to the Newtonian case. During the diastole the aforementioned behavior is reversed (Fig. 6).
CONCLUSION
The WSS and velocity distributions along of the abdominal bifurcation for a patient-specific in rest were investigated by using two different models for the blood viscosity, one Newtonian and other non-Newtonian. The non-Newtonian effects on the WSS are attributed to the constitutive relation given by Walburn-Schneck’s model that is based in the empirically observed blood rheology. The shear thinning behavior of the viscosity decreases the amplitude between higher WSS values generated during the systole and the lower WSS values generated during the diastole. Future work will extend these outcomes to others patient-specific and integrate non-Newtonian hemodynamics for patients subjected to exercise training.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
This article does not contain any studies with animals performed by any of the authors. All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
HUMAN AND ANIMAL RIGHTS
No animals were used for this study. All humans research procedures performed in the current study were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
CONSENT FOR PUBLICATION
Informed consent was obtained from all individual participants included in the study.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Gonzaga S was funded by INEGI’s scholarship ref “LIPOR_CIENER 67/14”.


